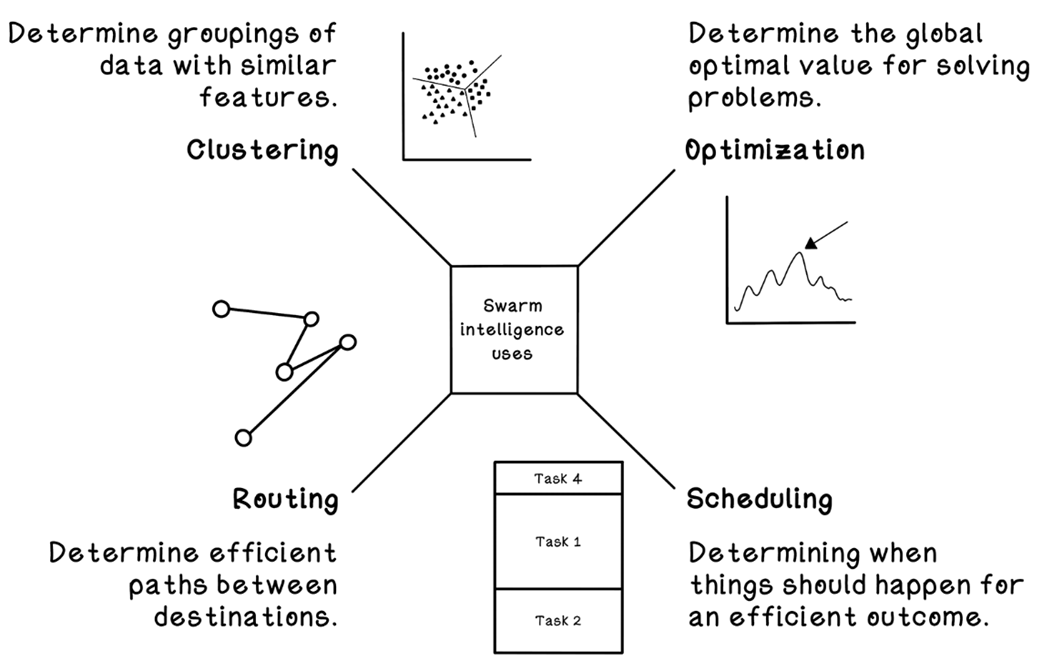
6 Swarm intelligence: Ants
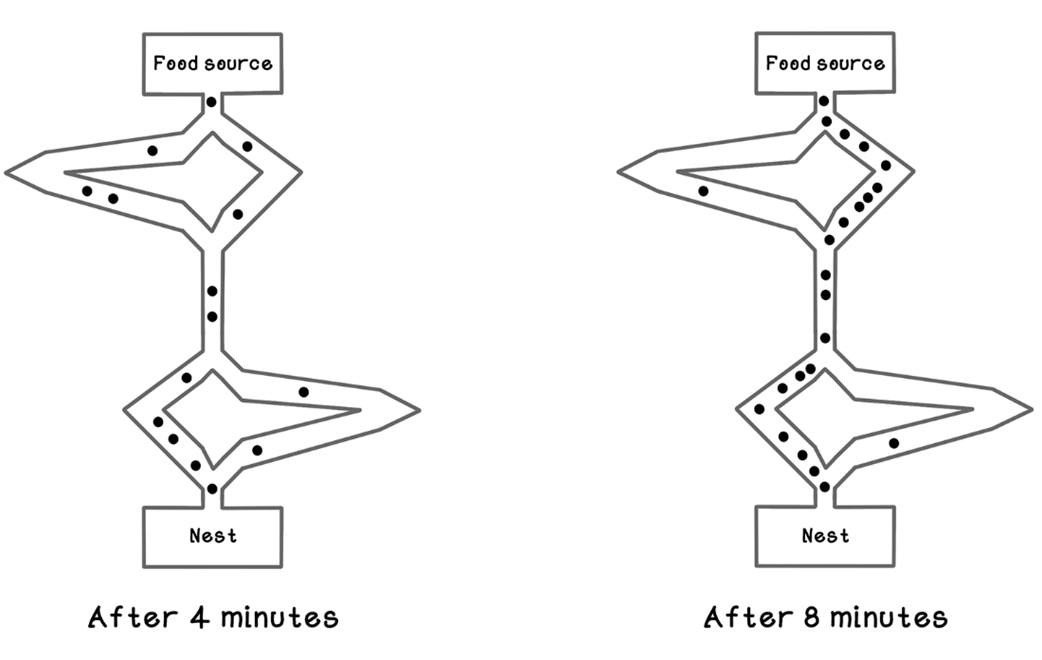
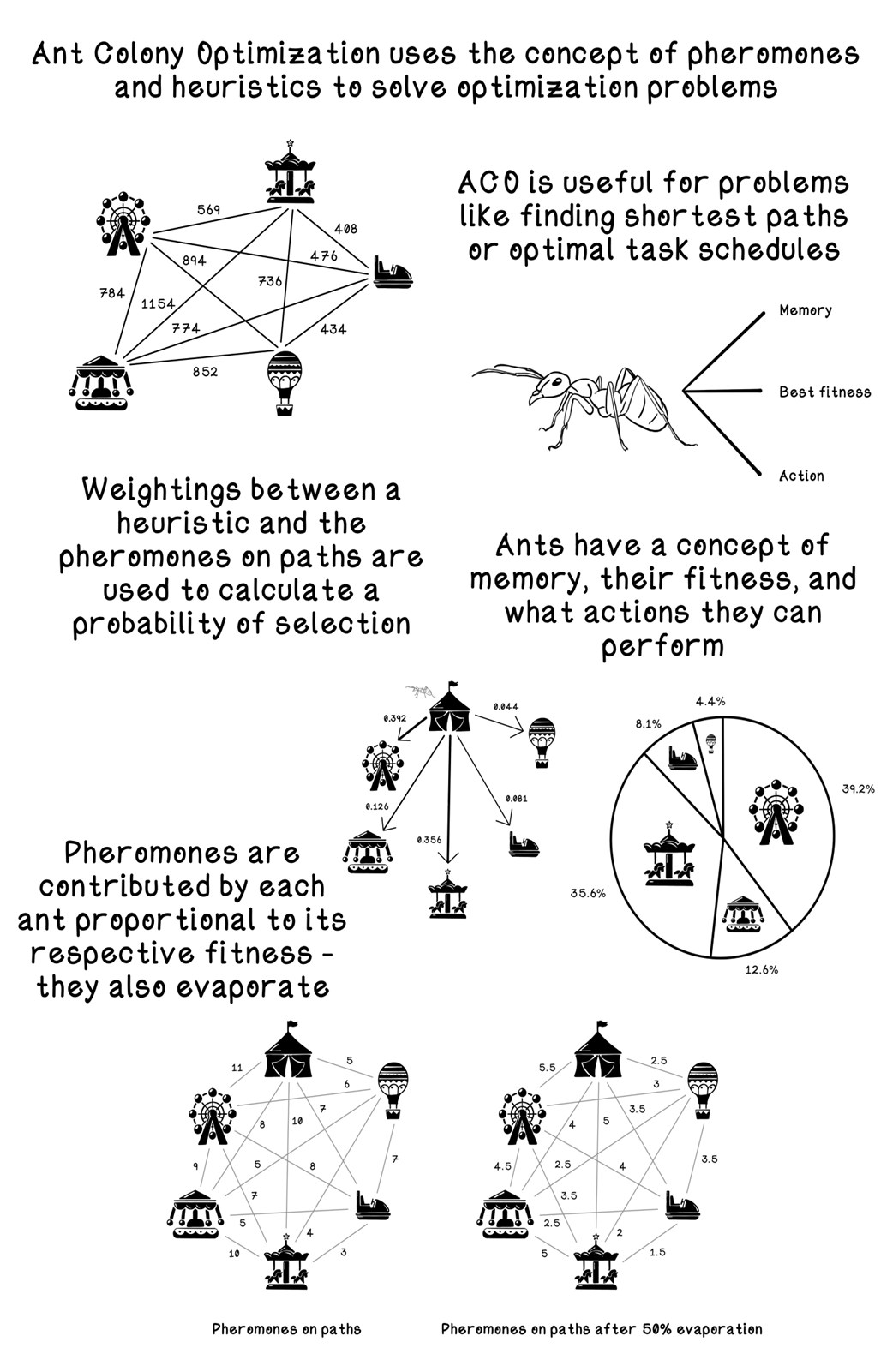
Swarm intelligence draws on simple, local interactions among many agents to yield surprisingly capable group behavior. Ants exemplify this: although individually limited, they coordinate via pheromone signals to build structures and, crucially, discover short routes to resources—an effect demonstrated by real-world experiments where colonies quickly converge on the shortest path. Ant colony optimization (ACO) abstracts this mechanism to tackle hard combinatorial optimization tasks in which exhaustive search is prohibitive, offering an alternative to other nature-inspired approaches such as genetic algorithms.
In the chapter’s running Carnival Problem (a traveling-tour analogue), the problem space is modeled with a distance matrix, while a parallel pheromone matrix records trail intensities. Each ant is an agent with memory of visited nodes, a running tour cost (fitness), and rules for choosing its next step. The ACO life cycle initializes uniform pheromones, places ants at random starts, and has them construct tours by balancing two signals: accumulated pheromones (collective experience) and a domain heuristic (for distances, typically inverse length), weighted by alpha and beta. A stochastic element encourages exploration, and roulette-wheel selection converts path scores into probabilistic choices. After each iteration, trails evaporate to prevent premature convergence and receive deposits proportional to tour quality, the best-so-far solution is updated, and the process repeats until a stopping criterion (fixed iterations or stagnation). Key parameters—evaporation rate, alpha/beta, number of ants, and iterations—govern the exploration–exploitation trade-off and runtime.
Beyond toy graphs, ACO applies to real routing and logistics with rich constraints, to job and shift scheduling by treating “locations” as tasks and encoding domain rules into the heuristic, and to image processing for edge detection by letting ants lay stronger trails along high-contrast pixel transitions. The approach scales better than brute force on large instances, adapts well through problem-specific heuristics, and benefits from careful tuning to balance solution quality against computation, making it a practical, general framework for complex optimization.
A group of ants working together to cross a chasm

Asymmetric bridge experiment
Problems addressed by swarm optimization
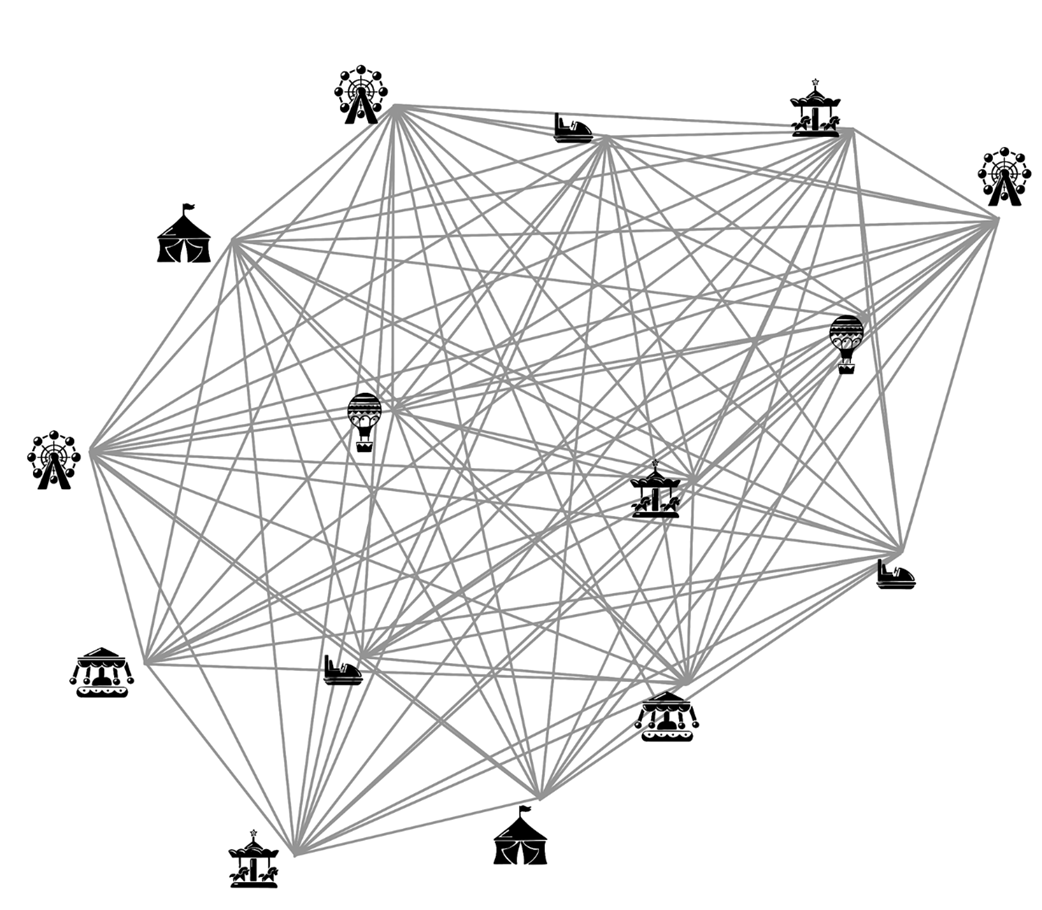
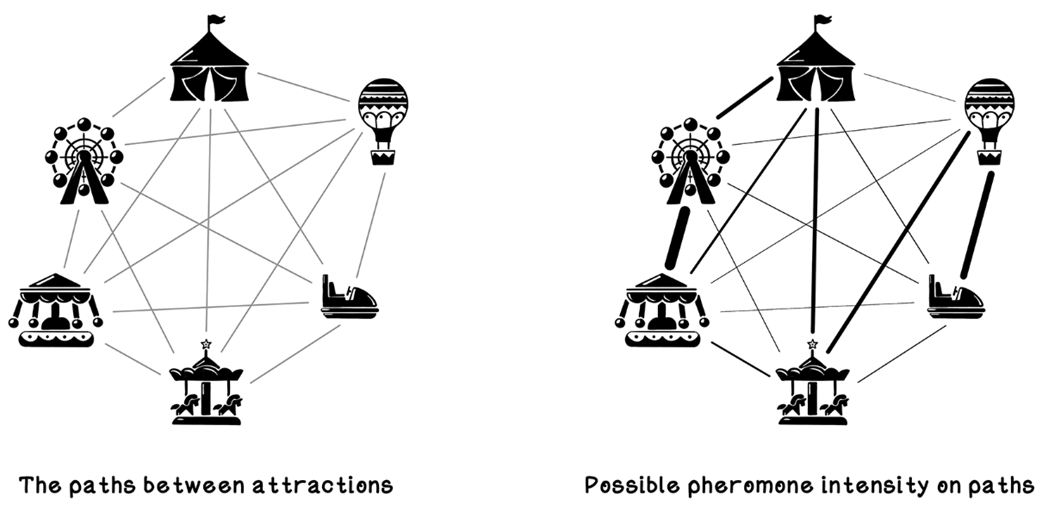
Carnival attractions and paths between them

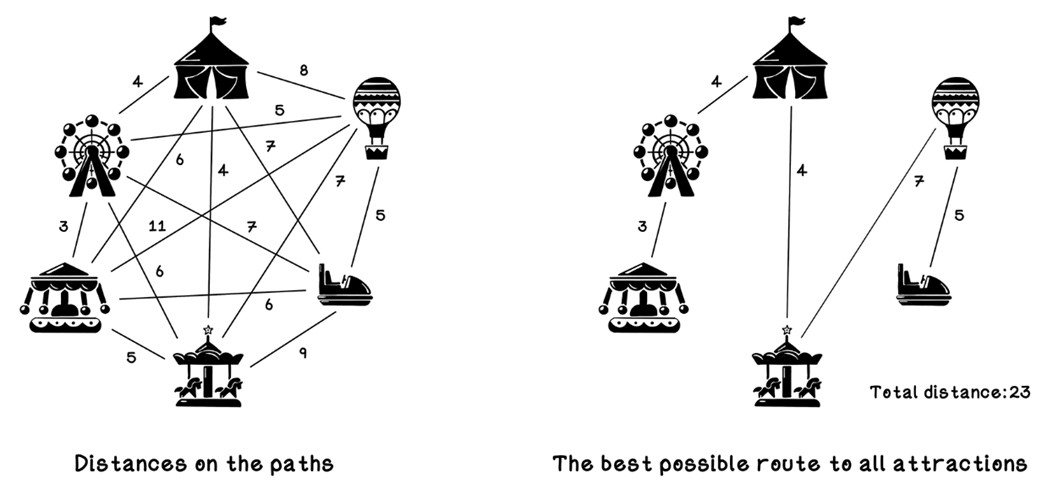
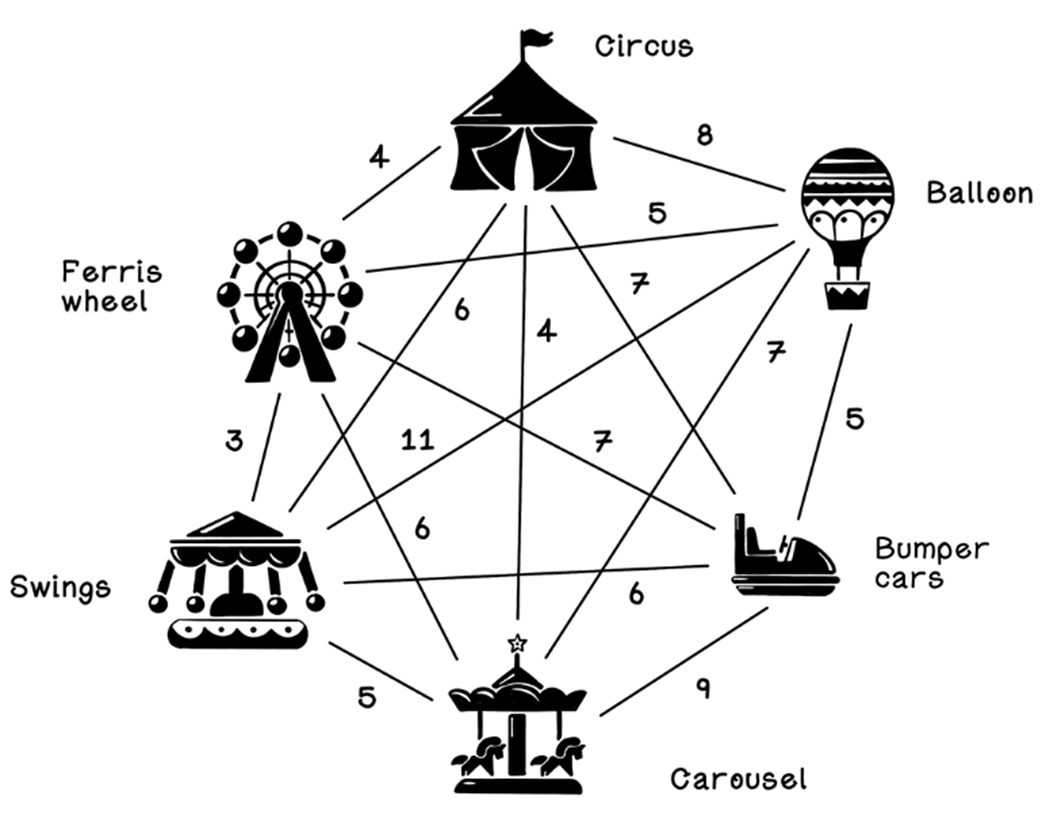
Distances between attractions and a possible path

Distances between attractions and an optimal path
A larger dataset of attractions and paths between them
An example of the Carnival Problem

Properties of an ant




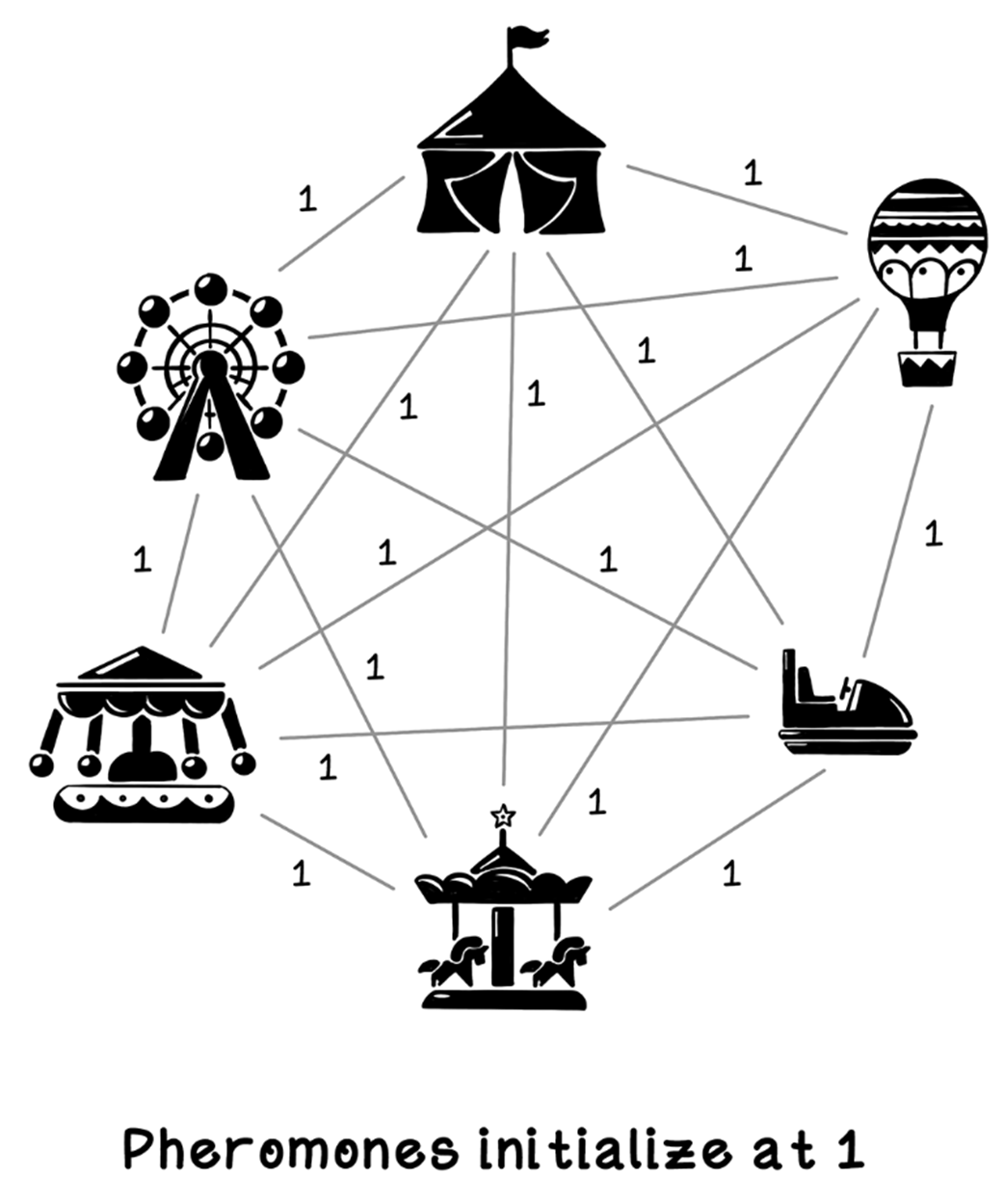
Example pheromone intensity on paths
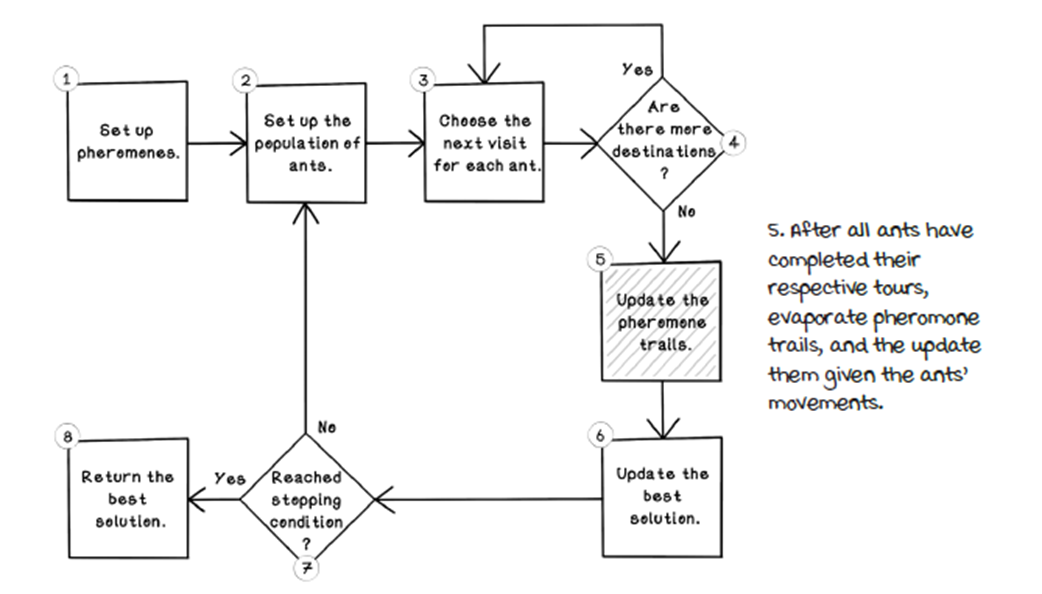
The ant colony optimization algorithm life cycle
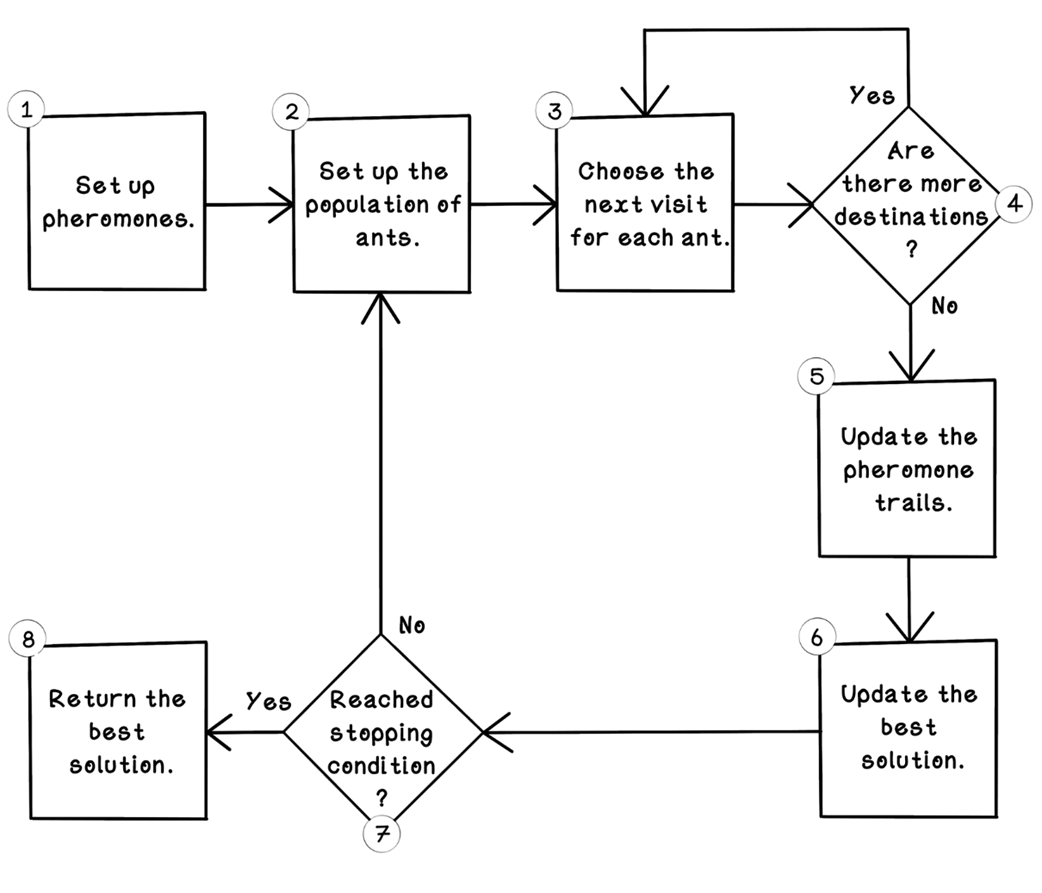
Set up the pheromones.
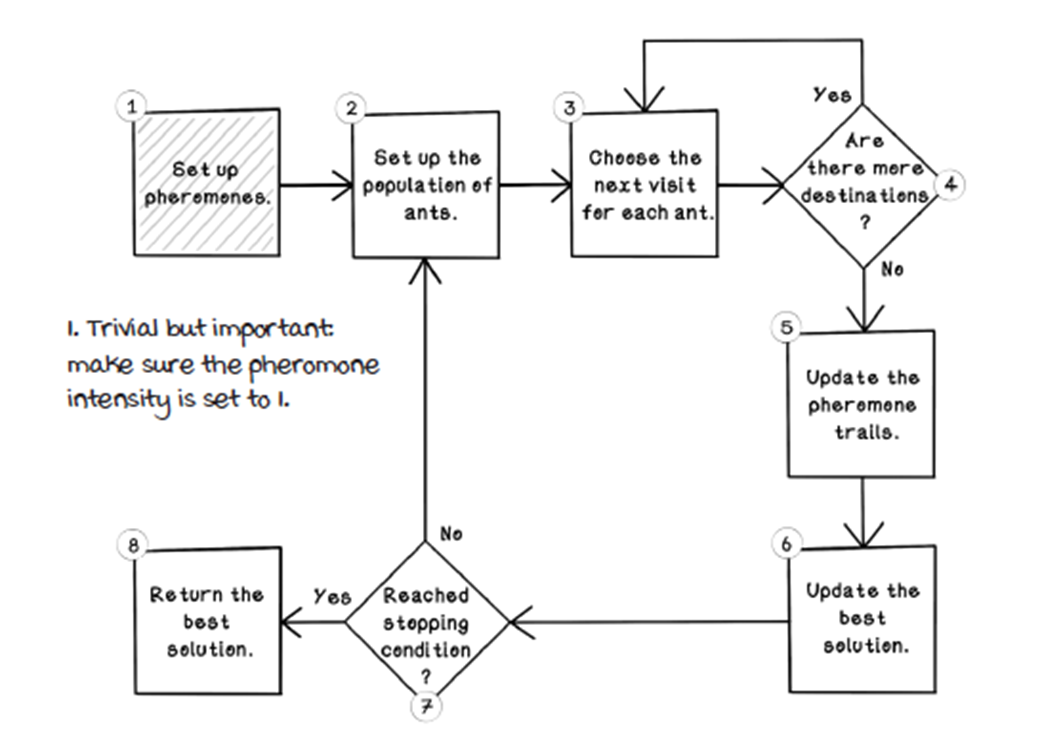
Initialization of pheromones

Set up the population of ants.
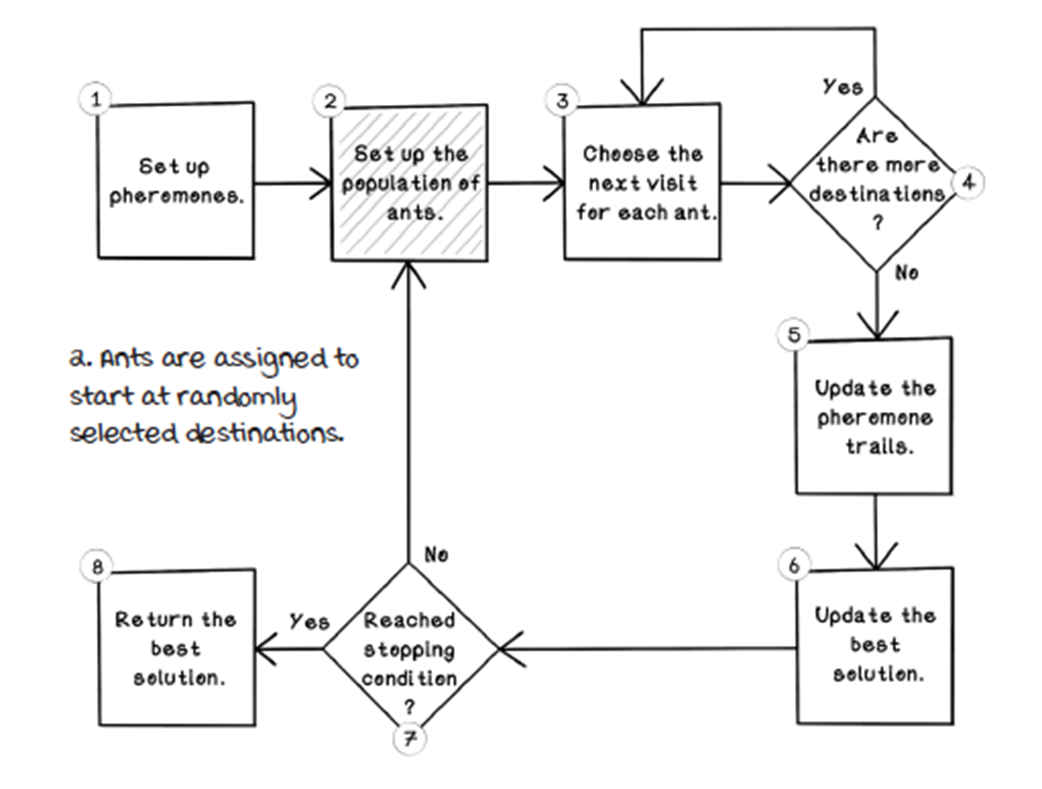
Ants start at random attractions.


Choose the next visit for each ant.
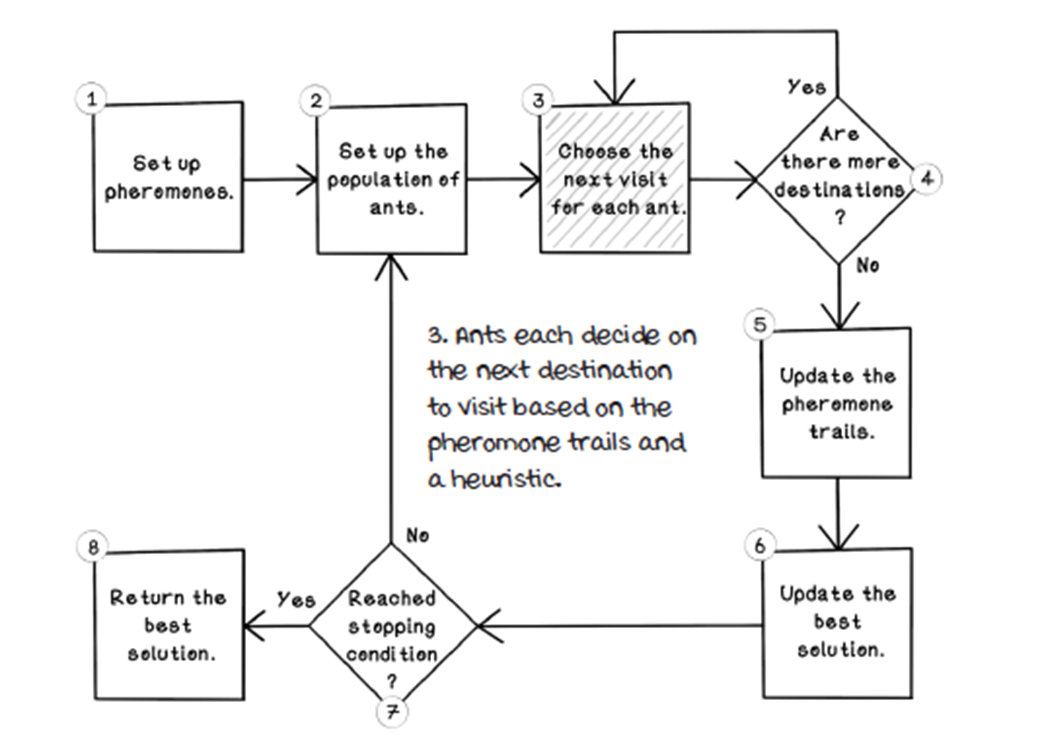
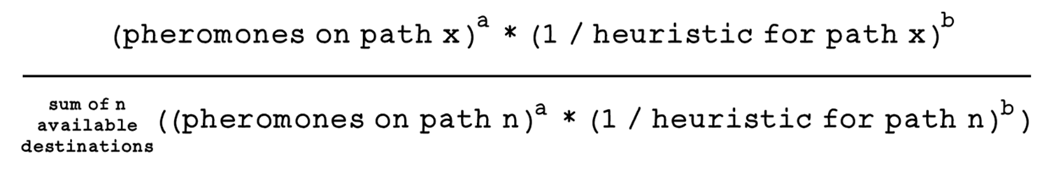
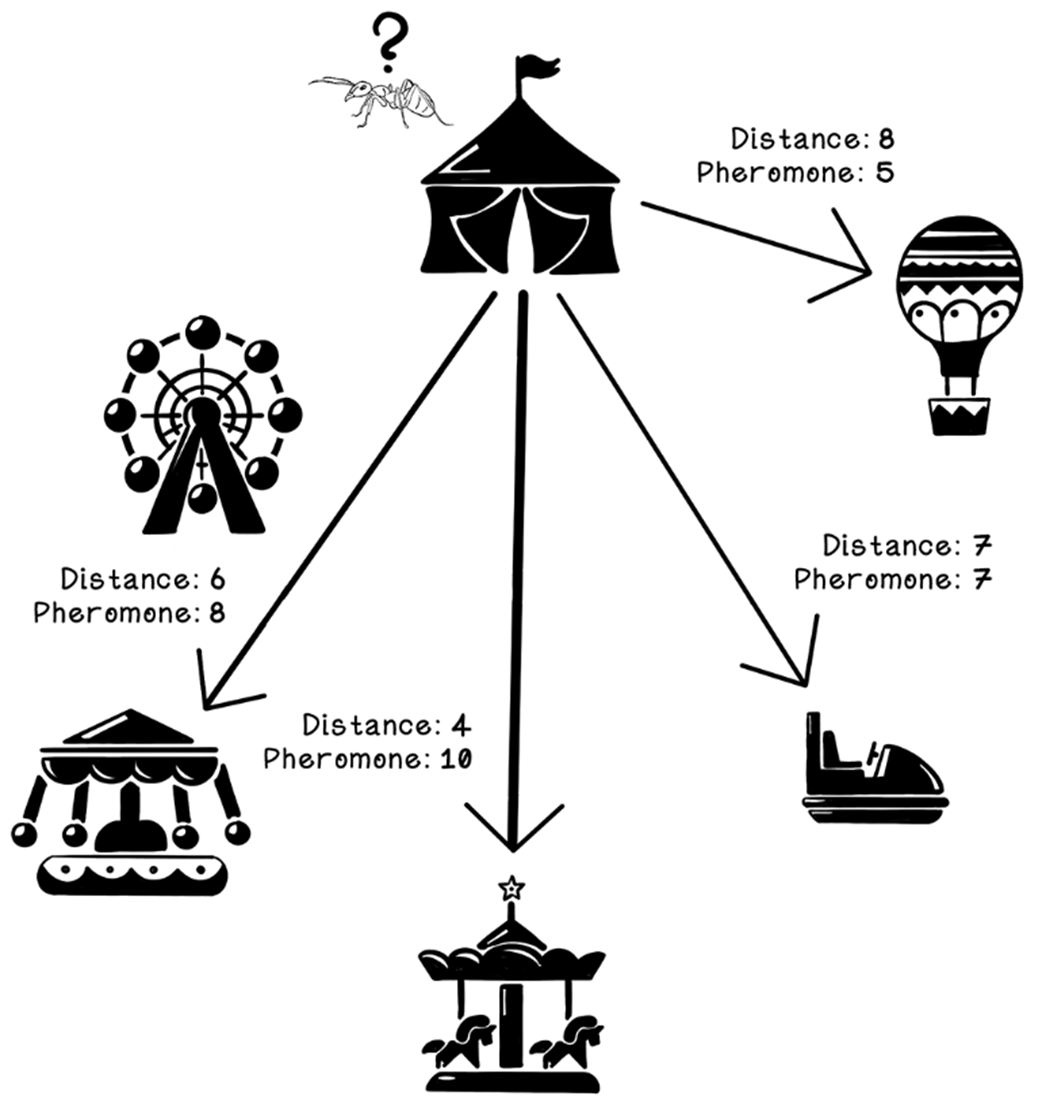
Example of possible paths from the circus
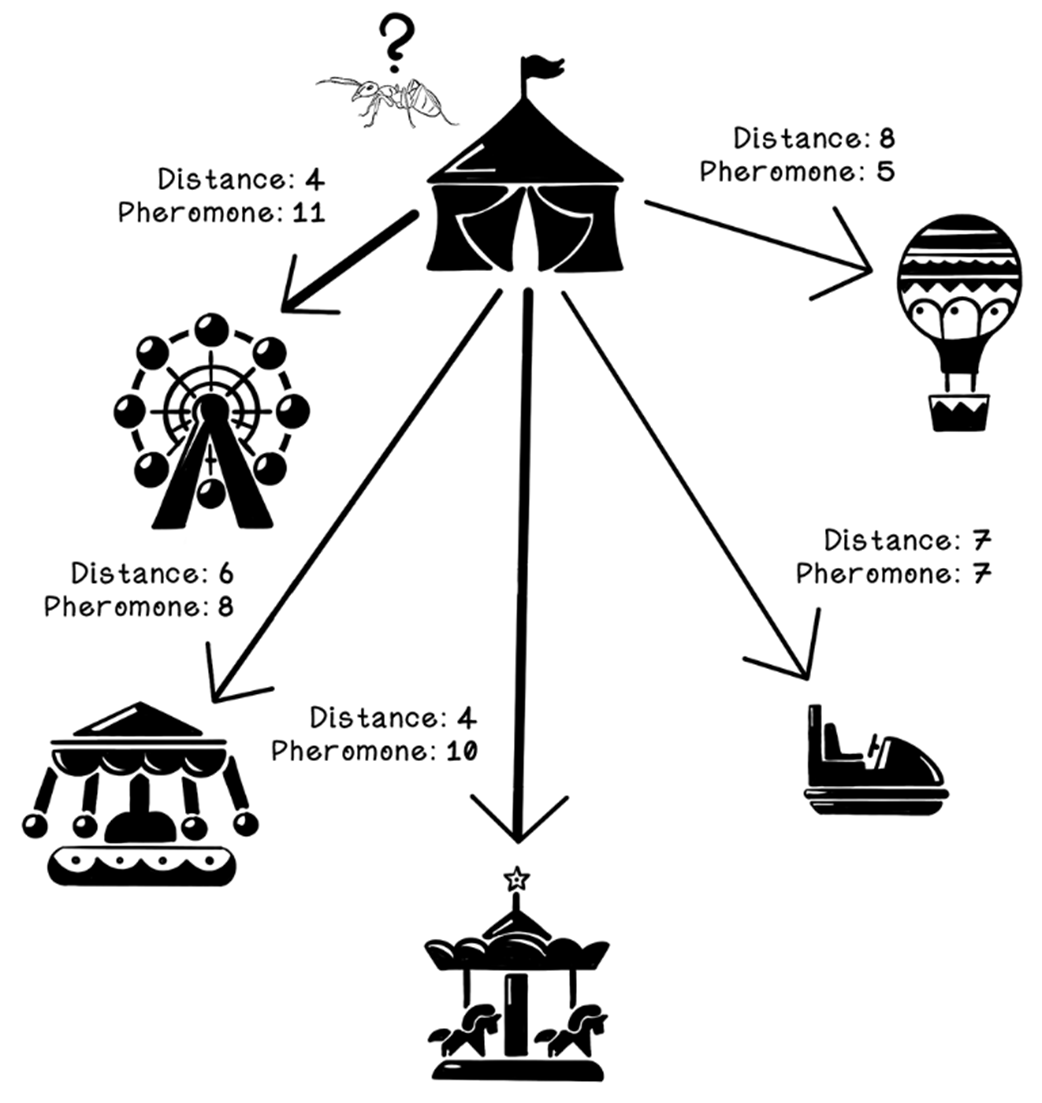
The pheromone influence and heuristic influence of the formula
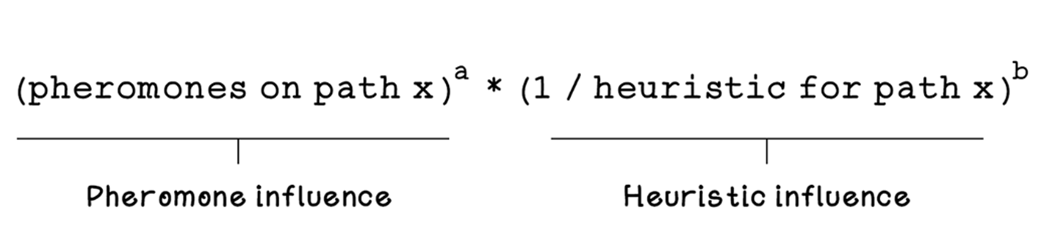
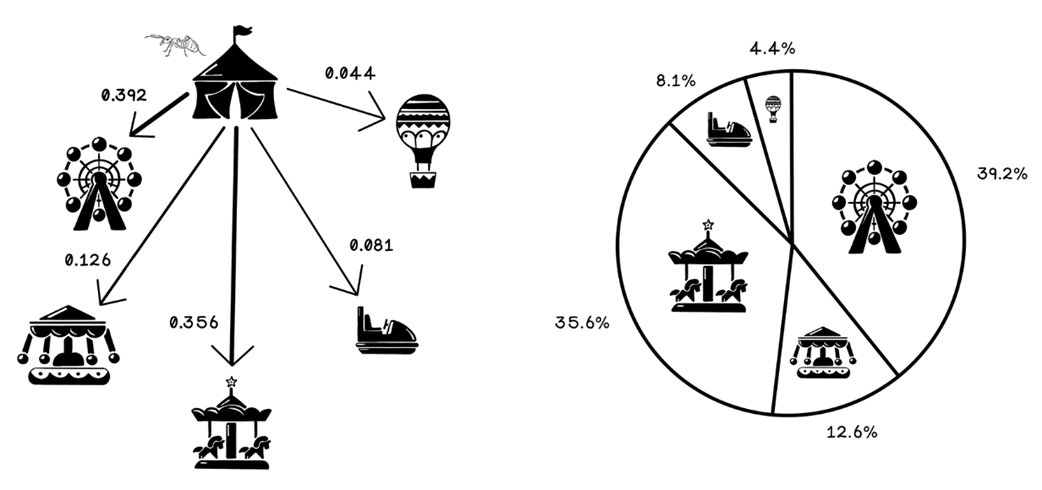
Probability calculations for paths

The final probability of each attraction being selected
Example of possible paths from the circus, excluding visited attractions
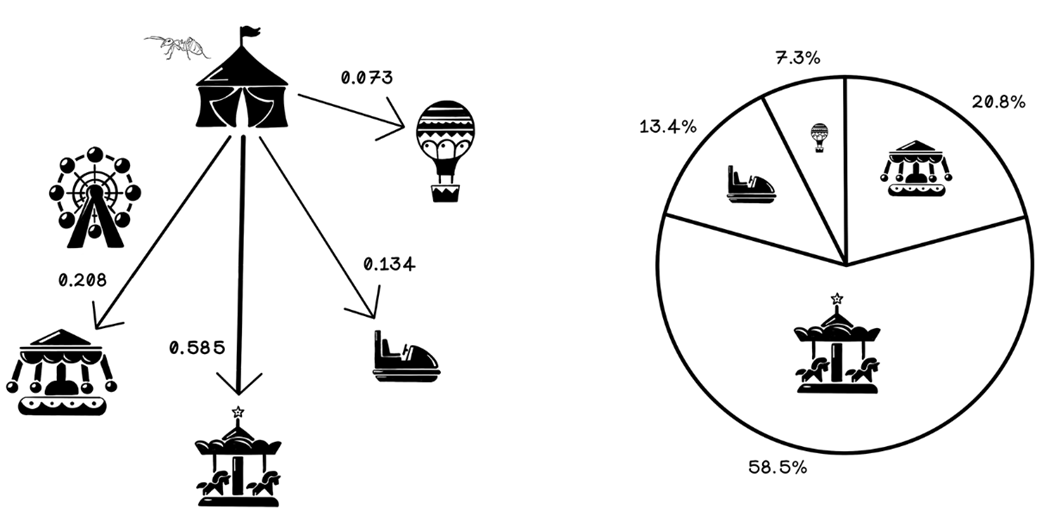
Probability calculations for paths

The final probability of each attraction being selected


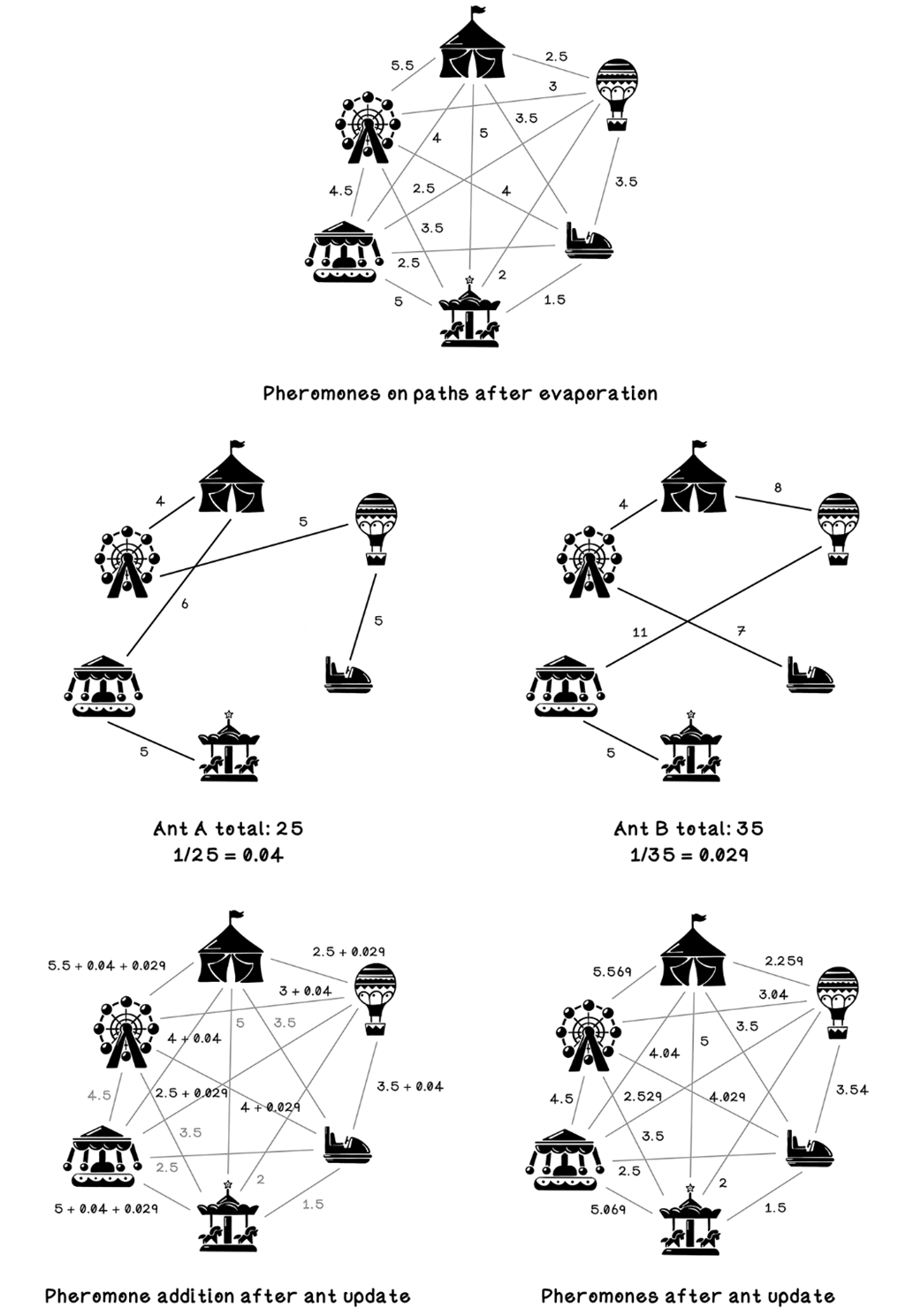
Update the pheromone trails.
Example of updating pheromone trails for evaporation
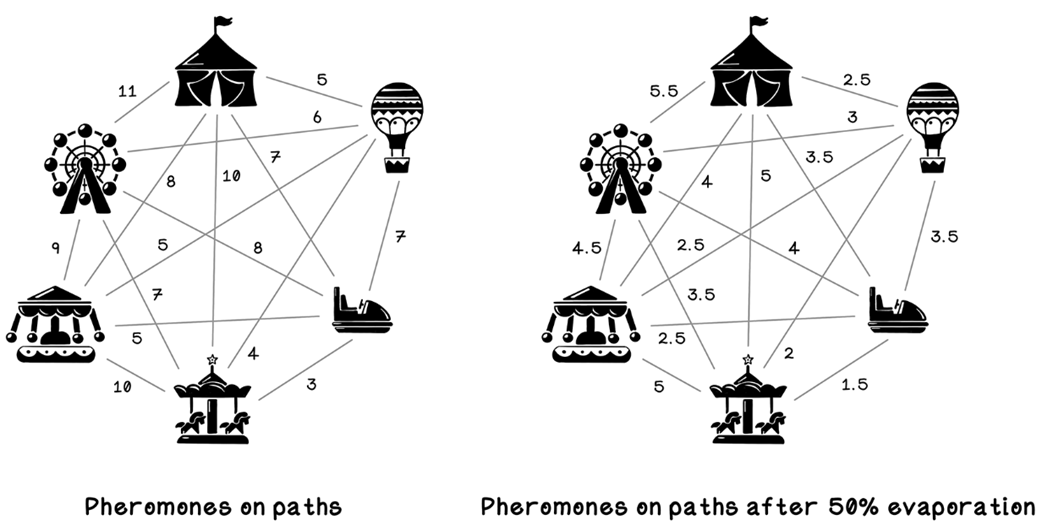
Pheromone updates based on ant movements

Update the best solution.

Reached stopping condition?

Parameters that can be tweaked in the ant colony optimization algorithm

Summary of ant colony optimization
FAQ
What is swarm intelligence and why are ants a good example?
Swarm intelligence refers to problem-solving behaviors that emerge from simple agents interacting locally, inspired by nature. Ants are a classic example: while individual ants are simple, colonies collectively find efficient paths, build structures, and coordinate via pheromones—chemical signals that guide other ants—leading to intelligent, emergent behavior.What kinds of problems does ant colony optimization (ACO) solve well?
ACO is well-suited to hard combinatorial optimization problems with huge search spaces and constraints where exact solutions are expensive, such as route planning (TSP-like tasks), scheduling (e.g., nurse shifts or compute jobs), and even image edge detection. It searches for high-quality solutions when brute force is impractical.How is the Carnival Problem modeled for ACO?
The carnival attractions form nodes in a fully connected graph; edges carry distances. Two matrices represent the state: a distance matrix holds pairwise distances between attractions, and a pheromone matrix holds trail intensities on each edge. Ants build tours that visit each attraction once, seeking the shortest total distance.What does an “ant” look like in the algorithm?
Each ant maintains: (1) memory of visited nodes (to avoid revisits within a tour), (2) its current tour and total distance (fitness), and (3) actions to choose the next node and to deposit pheromones along traveled edges.What is the life cycle of an ACO run?
- Initialize pheromone trails (typically uniform values like 1).- Create a population of ants with random start nodes.
- For each ant, construct a tour by repeatedly selecting the next node.
- Update pheromone trails via evaporation and deposition based on tours.
- Update the global best solution.
- Repeat for a set number of iterations or until convergence/stagnation.
 Grokking AI Algorithms, Second Edition ebook for free
Grokking AI Algorithms, Second Edition ebook for free