1 Starting a fabulous adventure
This opening chapter sets the tone for a tour of algorithms and data structures that are “fabulous” not just for their efficiency, but for their surprise, breadth, and joy. The author highlights qualities such as solving real problems beyond canned library solutions, embracing counterintuitive ideas like immutability to gain robustness and simplicity, and recognizing patterns that transfer across domains—backtracking powering tree search, map coloring, sudoku, and code formatting. The narrative emphasizes writing code that expresses meaning over mechanism, delight in trick-like designs (such as structures that seem to hold no data), leveraging language features to their fullest, reframing problems for dramatic gains (e.g., HashLife), connecting practice to theory, and keeping a spirit of fun.
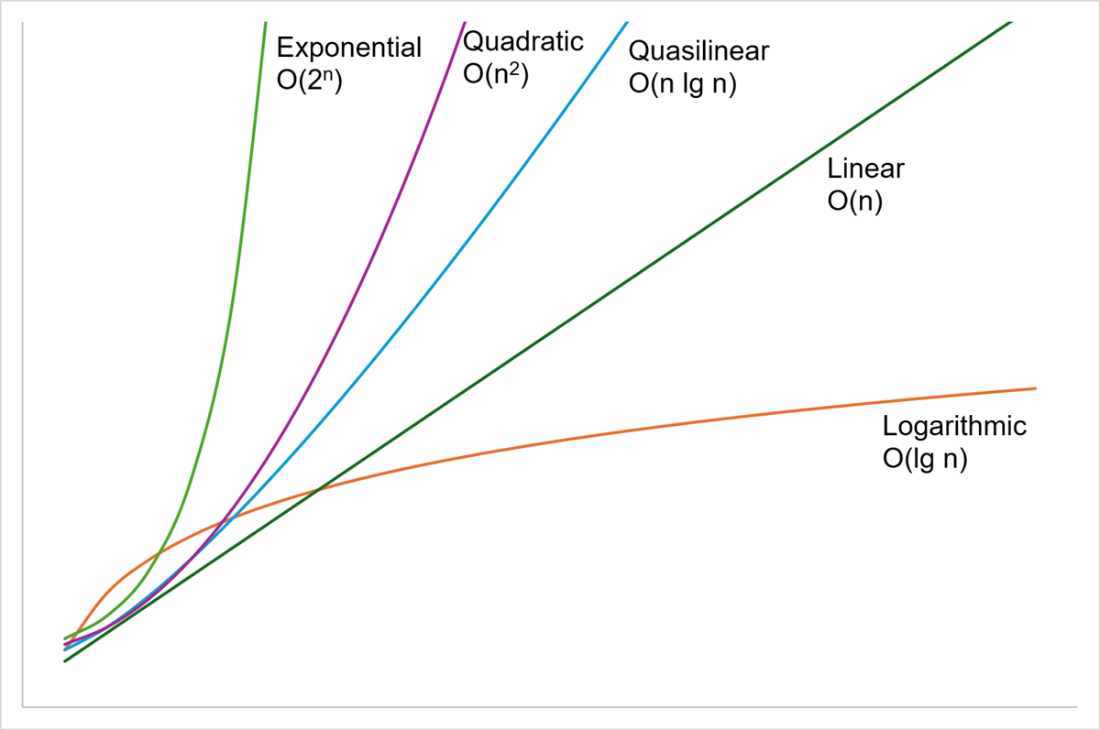
Foundational concepts are briefly defined: a data structure organizes information; an algorithm is a finite sequence of steps (possibly randomized) that solves a problem; complexity characterizes how cost grows with input size. Big-O notation frames common growth rates from constant and logarithmic through linear, quasilinear, quadratic, and intractable exponential/factorial behaviors. The discussion stresses that “size” must be specified (e.g., tree height versus node count), “cost” includes more than time (memory and other resources matter), and best/average/worst cases can diverge. A cautionary note: asymptotically superior algorithms are not automatically better for typical, small inputs—practical workloads and constants often dominate.
A warm-up explores an immutable linked list in C#, using a simple reverse routine that runs in linear time and space. This example doubles as a performance audit: constructing lists is linear overall, equality and emptiness checks can hide costs or recursion pitfalls in generated code, and naive string concatenation leads to accidental quadratic behavior. With these lessons in hand, the journey proceeds through familiar structures (stacks, queues, trees) with novel twists—persistence, memoization, elegant reordering techniques, and even a seemingly constant-time list reversal—then to backtracking, unification and anti-unification, and finally a practical toolbox for probability and Bayesian inference. Although implemented in C#, the ideas generalize across mainstream languages, and subsequent chapters dig deeper into immutable lists and their surprising variants.
A graph comparing the growth curves for logarithmic, linear, quasilinear, quadratic and exponential growth. Logarithmic is the shallowest curve, growing very slowly, and exponential is the fastest.
Summary
- There are lots of books about standard data structures such as lists, trees and hash tables, and the algorithms for sorting and searching them. And there are lots of implementations of them already in class libraries. In this book we’ll look at the less well-known, more off-the-beaten-path data structures and algorithms that I had to learn about during my career. I’ve chosen the topics I found the most fabulous: the ones that are counterintuitive, or seemingly magical, or that push boundaries of languages.
- I had to learn about almost all the topics in this book when I needed a new tool in my toolbox to solve a job-related problem. I hope this book saves you from having to read all the abstruse papers that I had to digest if you too have such a problem to solve.
- But more important to me is that all these fabulous adventures gave me a deeper appreciation for what computer programmers are capable of. They changed how I think about the craft of programming. And I had a lot of fun along the way! I hope you do too.
- Asymptotic complexity gives a measurement of how a solution scales to the size of the problem you’re throwing at it. We generally want algorithms to be better than quadratic if we want them to scale to large problems.
- Complexity analysis can be subtle. It’s important to remember that time is not the only resource users care about, and that they might also have opinions on whether avoiding a bad worst-case scenario is more or less important than achieving an excellent average performance.
- If problems are always small, then asymptotic complexity matters less.
- Reversing a linked list is straightforward if you have an immutable list! We’ll look at other kinds of immutable lists next.
FAQ
What does this chapter mean by “fabulous” algorithms and data structures?
They solve real problems off the beaten path, sometimes with counterintuitive ideas (like immutability for undo/redo), apply across many domains (e.g., backtracking for maps, Sudoku, and pretty printing), emphasize high-level meaning over low-level mechanisms, feel like clever “magic” (Hughes list), leverage language features to the fullest (e.g., C# generics), reframe problems for big wins (HashLife), connect practice with theory (category-like patterns), and they’re fun to build.How does the chapter define a data structure, an algorithm, and complexity?
A data structure organizes information; an algorithm is a finite procedure (not necessarily deterministic or executed by a computer) to solve a problem; complexity relates problem size to resource cost (time, memory, etc.).What are common Big-O complexities and intuitive examples?
- O(1): read the first element of an array.
- O(log n): identifier length grows with log n; rarely the bottleneck in practice.
- O(n): summing n integers.
- O(n log n): typical comparison sorting.
- O(n²): naive repeated string concatenation; avoid “accidentally quadratic” code.
- O(2ⁿ), O(n!): combinatorial explosions; intractable beyond tiny inputs.
How should I choose “n” and what costs matter?
Pick a size measure that matches the problem (e.g., for trees, height vs. node count should be stated). Consider time and non-time resources (memory, handles, etc.), and distinguish best-, average-, and worst-case behavior.Why isn’t the asymptotically “best” algorithm always the right choice?
Real workloads may be small and simple, where a naive approach with worse worst-case complexity is faster due to lower constants and simpler code paths. Optimize for the inputs you actually have, not only for asymptotics.How is the immutable linked list represented, and why avoid null for emptiness?
The empty list is a valid object (not just null) so you can safely call methods on it. A simple representation uses a node withValue = null and Tail = null for empty, but that opens the door to invalid states if misused; later chapters improve this design.What performance traits should I know about the list’s construction and methods?
- Pushing/constructing a node is O(1); building n nodes is O(n) time and memory.
- A naive
ToStringthat repeatedly concatenates is O(n²); preferStringBuilderfor O(n). - Record types auto-generate value equality; comparing two lists can be O(k) for the shared prefix and is recursive, risking stack overflow on long equal prefixes—consider custom, non-recursive equality.
IsEmptyvia record equality is needlessly expensive;IsEmpty => Tail == nullis cheaper.
 Fabulous Adventures in Data Structures and Algorithms ebook for free
Fabulous Adventures in Data Structures and Algorithms ebook for free