1 The advantages and challenges of programming quantum computers

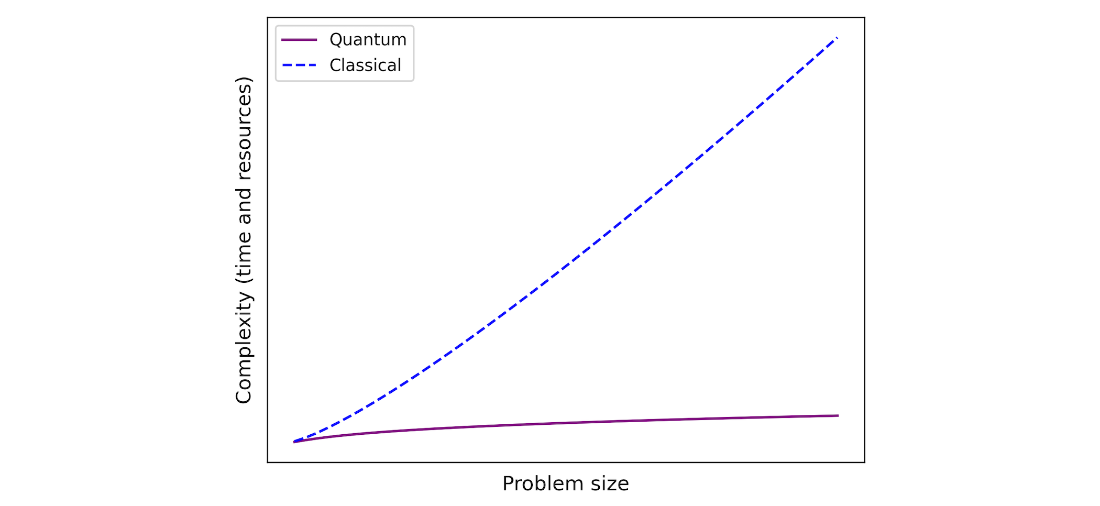
Quantum computing promises substantial gains for carefully chosen tasks by exploiting forms of speedup that outpace classical scaling, as in Fourier-transform-based workloads and other compute-intensive problems. Beyond raw acceleration, quantum devices can tackle computations that are impractical or impossible classically, such as simulating quantum physical and chemical systems or producing truly random samples from complex probability distributions. Since the late 1980s, ideas from Feynman and Manin catalyzed interest in quantum advantage; today, maturing hardware and manufacturing are accelerating adoption and creating demand for developers who can recognize where quantum, classical, or hybrid approaches fit. This chapter sets expectations: it emphasizes applied mathematics and software techniques over physics, so practitioners can become “quantum ready” and translate familiar computer science abstractions into quantum programs.

The chapter identifies two pillars of quantum advantage: quantum parallelism and measurement. Quantum parallelism lets a single instruction act on many value pairs at once, akin to an unlimited SIMD model, which can yield dramatic reductions in the number of required operations; however, its broad-brush action often requires compensating steps to prevent unwanted side effects. Measurement is inherently non-deterministic: a single run yields one outcome drawn from a probability distribution defined by the quantum state, and repeated “shots” reveal the distribution. Results are typically read as binary strings (and often interpreted as integers), enabling either digital encodings of answers or probabilistic estimates. Together, these properties enable both speed and capability gains, while introducing practical considerations like repeated runs, verification, and careful control of how parallel updates shape the final outcome probabilities.

From a programmer’s perspective, a quantum computation evolves a state—a list of probabilities-with-direction over all possible outcomes—through sequences of elementary operations that recombine pairs of values (a “butterfly” pattern), then performs a measurement that collapses the superposition to a single outcome. The number of outcomes grows exponentially with qubits, but operations still update all relevant pairs in parallel; programming becomes the art of choosing the right sequence of elementary instructions so that measurement statistics encode the solution. The chapter closes by outlining three recurring patterns: sampling from hard-to-generate distributions; searching for digitally encoded solutions (e.g., Grover’s algorithm, and period-finding in Shor’s algorithm); and estimating probabilities for analog encodings via many shots, sometimes at significant cost if converted to digital form. These concepts equip developers to spot problems suited to quantum or hybrid solutions and to work in a hardware- and library-agnostic way as the ecosystem matures.

Comparison of the increase in computational complexity for computing Fourier transforms.

Visualization of the classical implementation for swapping consecutive values.

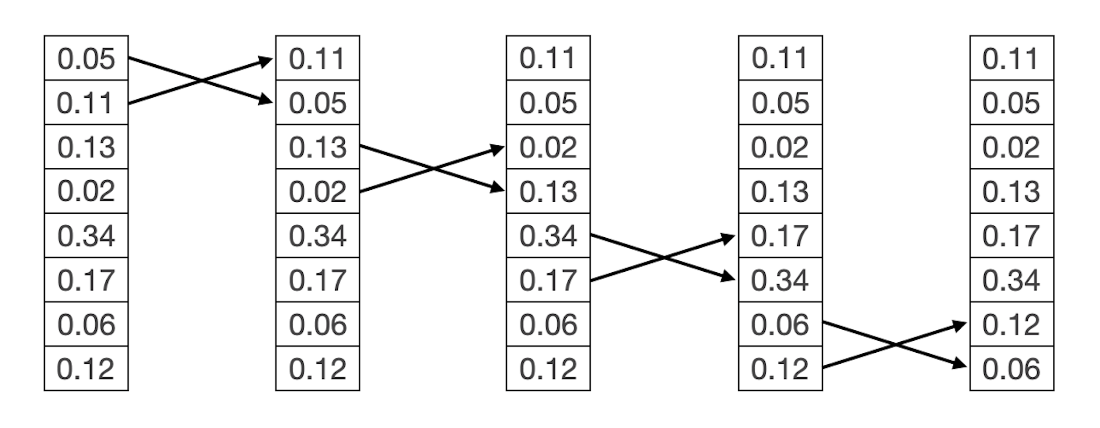
Visualization of the quantum implementation for swapping consecutive values.

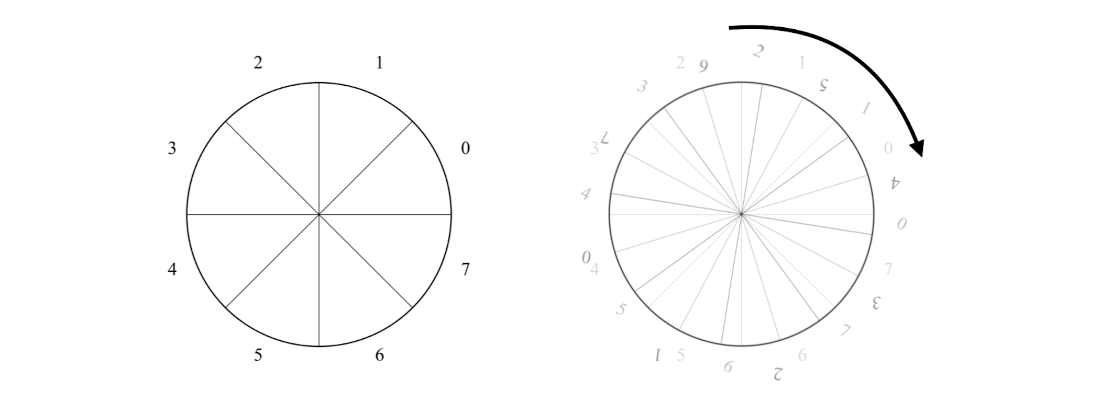
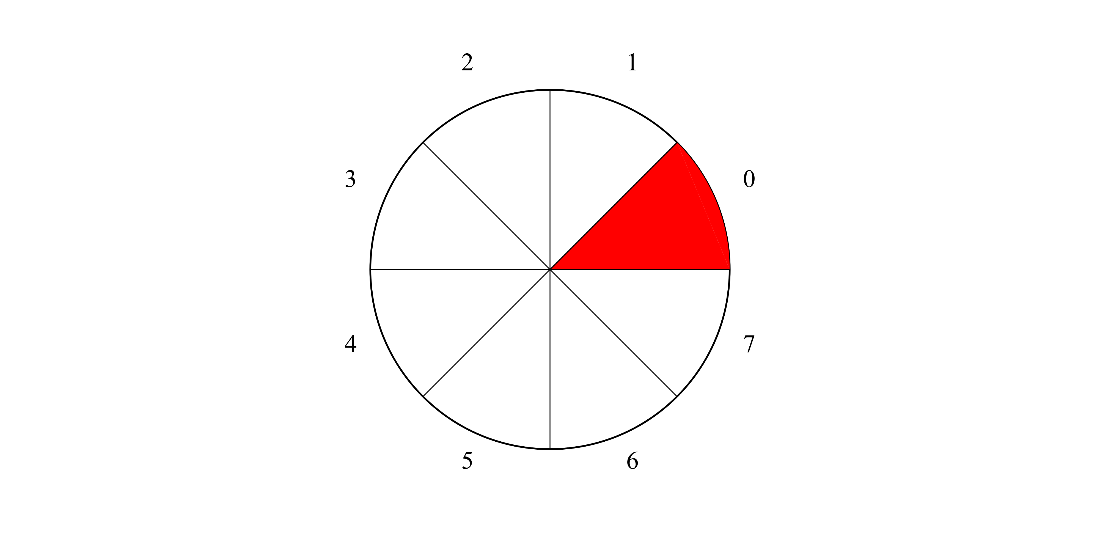
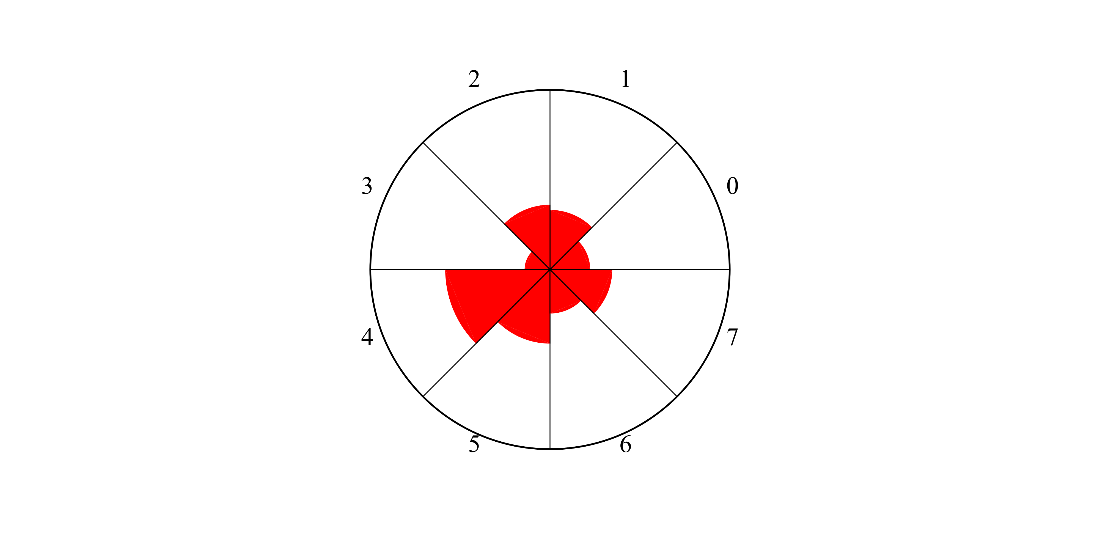
A circle divided into equal sectors, where the sectors represent each possible outcome of a certain quantum computation.

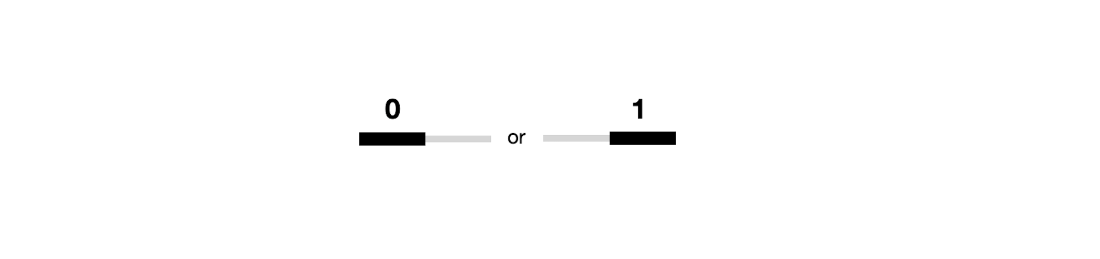
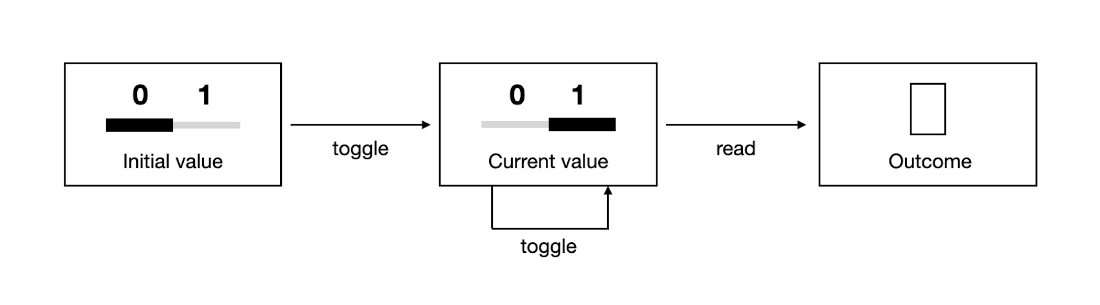
A classical bit works like a toggle or switch between 0 and 1.

The stages of a computation using a classical bit.

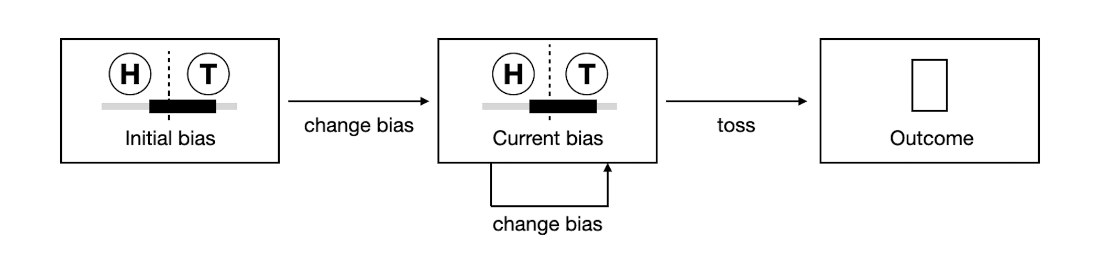
A quantum bit, or variable-bias coin, works like a slider that changes the probability of getting heads or tails.

The stages of a computation with a quantum bit.

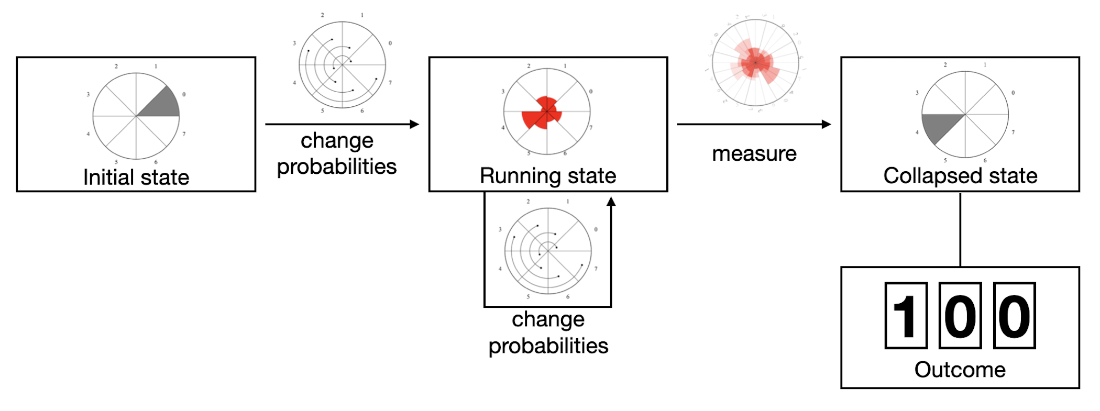
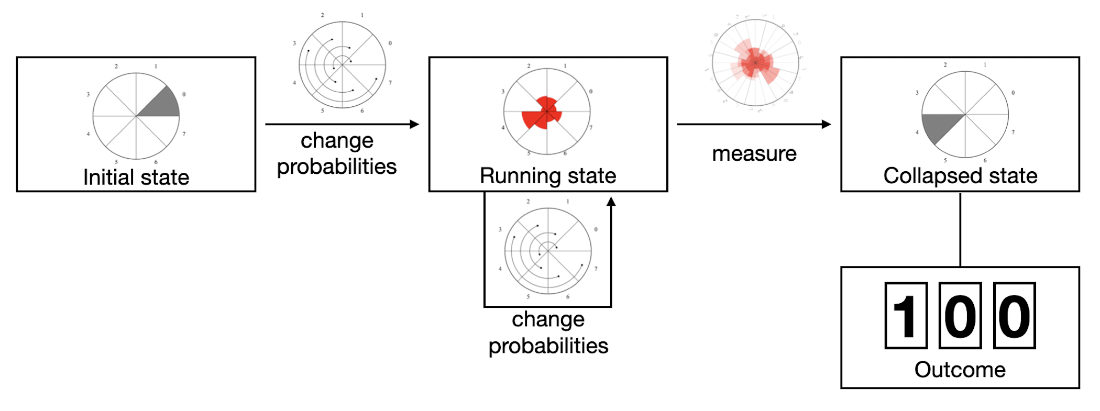
The steps of a quantum computation.

A wheel representation of a three-qubit quantum state in its initial state.

A rose chart representation of the probabilities associated with the outcomes of a three-qubit quantum system.

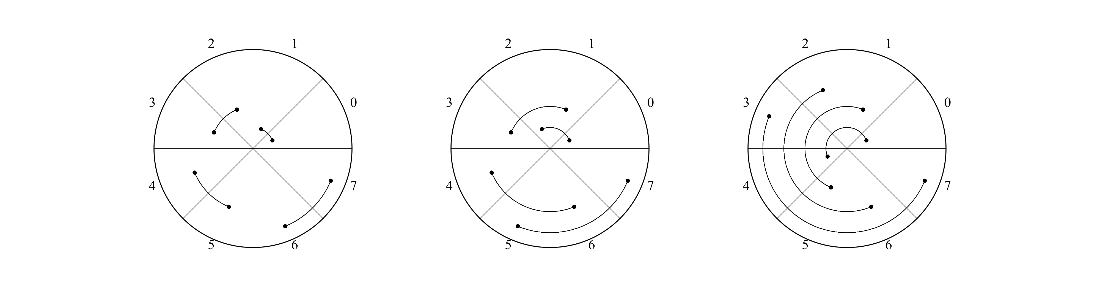
The possible pair combinations of a three-qubit system.

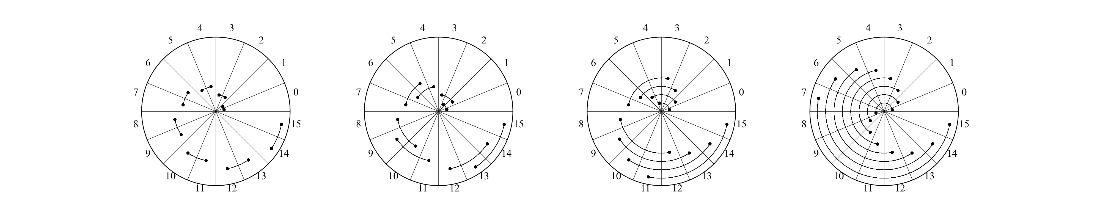
The possible pair combinations of a four-qubit system.

The steps of a quantum computation.

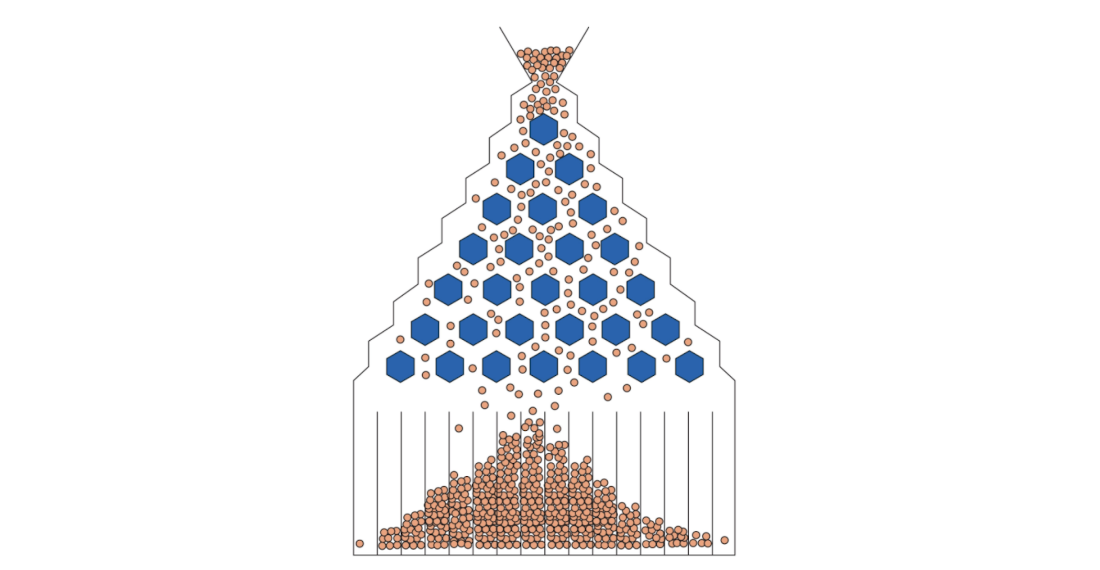
A Galton board showing physical pegs driving marbles into bins according to the binomial distribution.

• To be “quantum ready” you need to understand the mechanisms of quantum advantage and which problem types they can help with versus classical computing.
• Quantum parallelism and measurement can provide a quantum advantage over classical methods.
• In a quantum computation, pairs of probabilities are changed simultaneously, and computation outcomes are selected according to these probabilities. Quantum computations have the following distinct characteristics:
  • The state of a quantum computation consists of a probability-with-direction for each possible outcome.
  • Elementary computing instructions change pairs of probabilities-with-direction in parallel (using the butterfly computational model/pattern).
  • Quantum measurement is like sampling all possible outcomes according to their probabilities through repeating the same computation.
• There are three main quantum computing patterns: sampling from probability distributions, searching for optimal values, and estimating the probability of certain computation outcomes.

FAQ