1 Introduction to Bayesian statistics: Representing our knowledge and uncertainty with probabilities

This chapter introduces Bayesian statistics as a practical language for reasoning and decision-making under uncertainty. It motivates probability through a weather-forecasting example, contrasting a yes/no predictor with probabilistic forecasts that convey confidence and support different risk preferences. By modeling unknowns as random variables—binary, categorical, or continuous—probability lets us express beliefs at useful levels of granularity, compute summaries like expected values, and make more trustworthy, calibrated predictions. The chapter also highlights why uncertainty matters in modern AI: non-probabilistic models (e.g., standard neural networks) can be overconfident and fragile, whereas probabilistic reasoning provides a principled way to reflect noise, small datasets, and real-world risk.

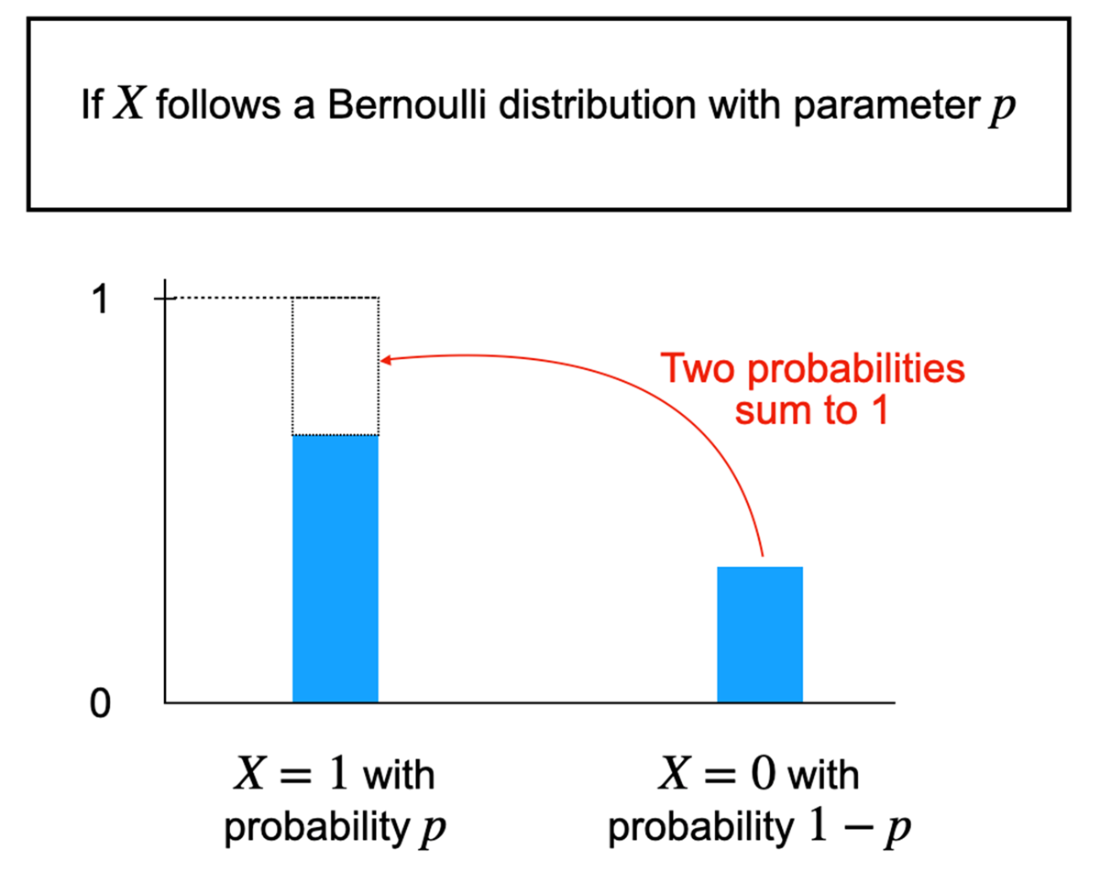
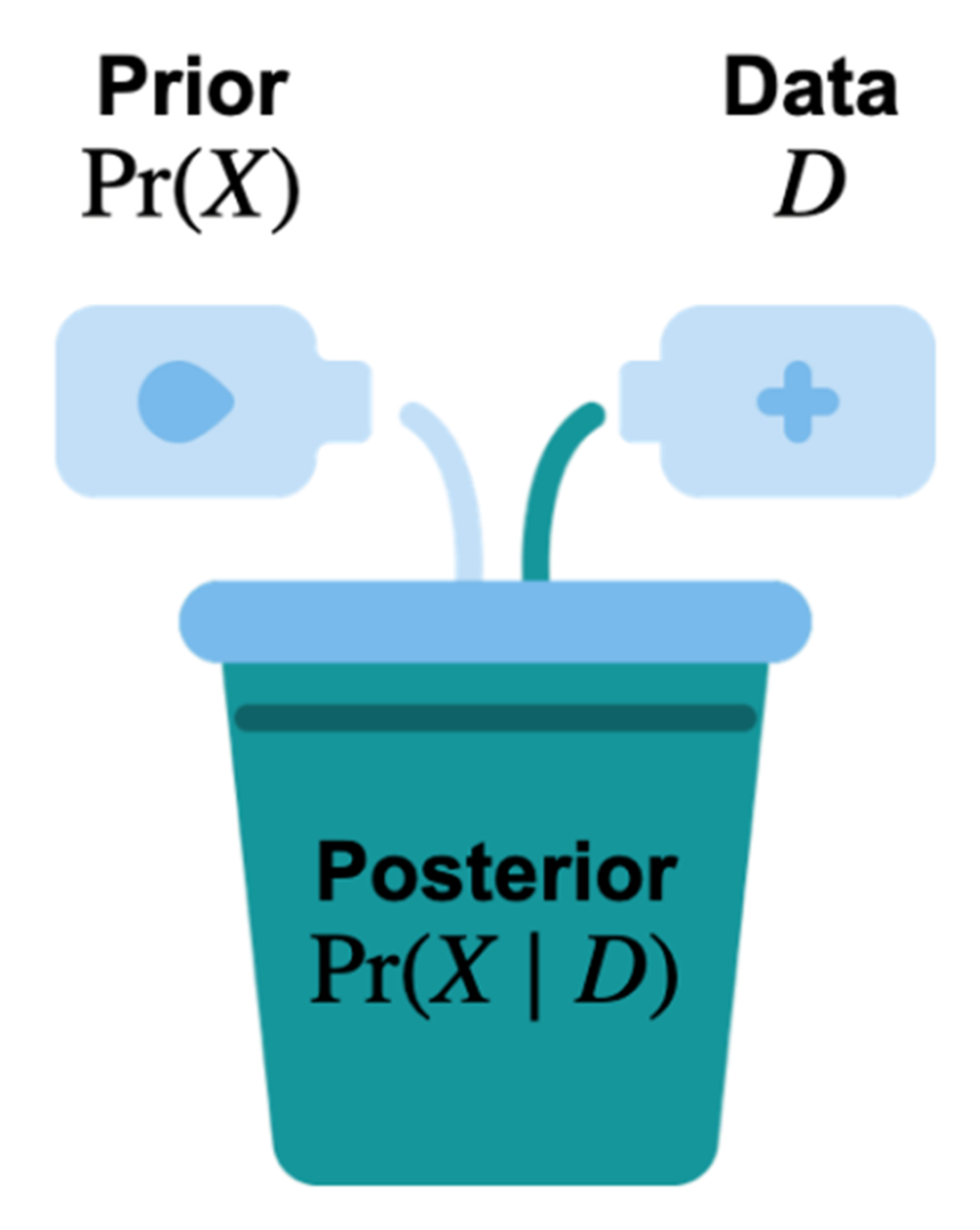
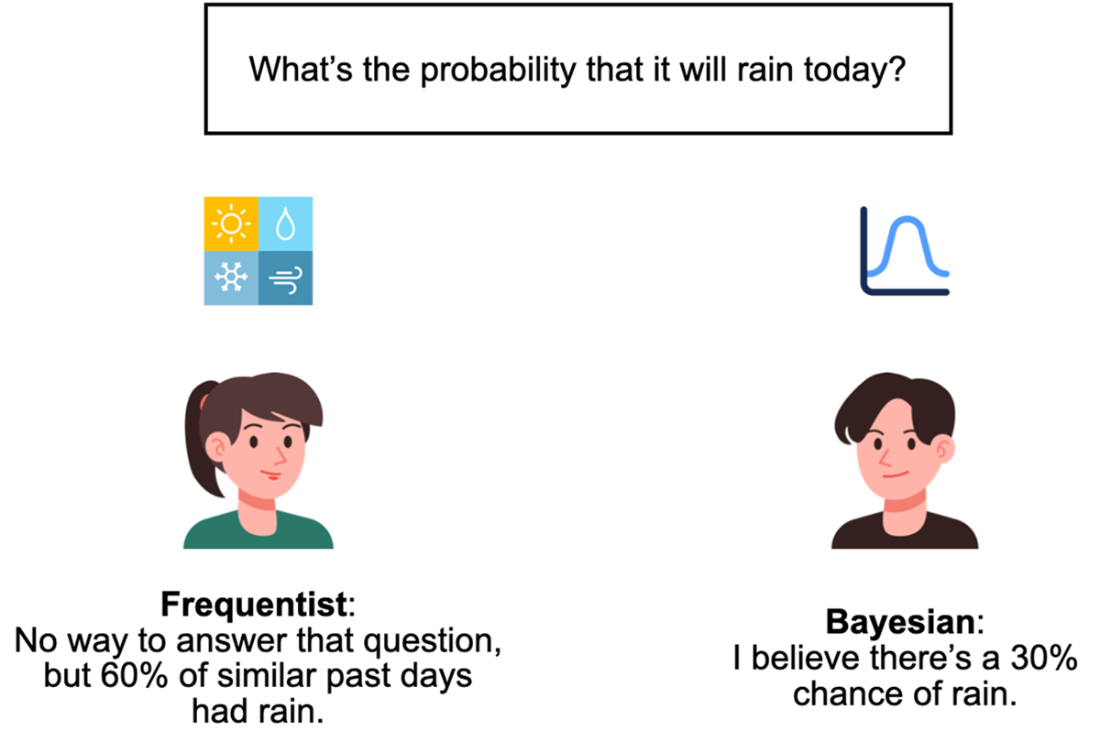
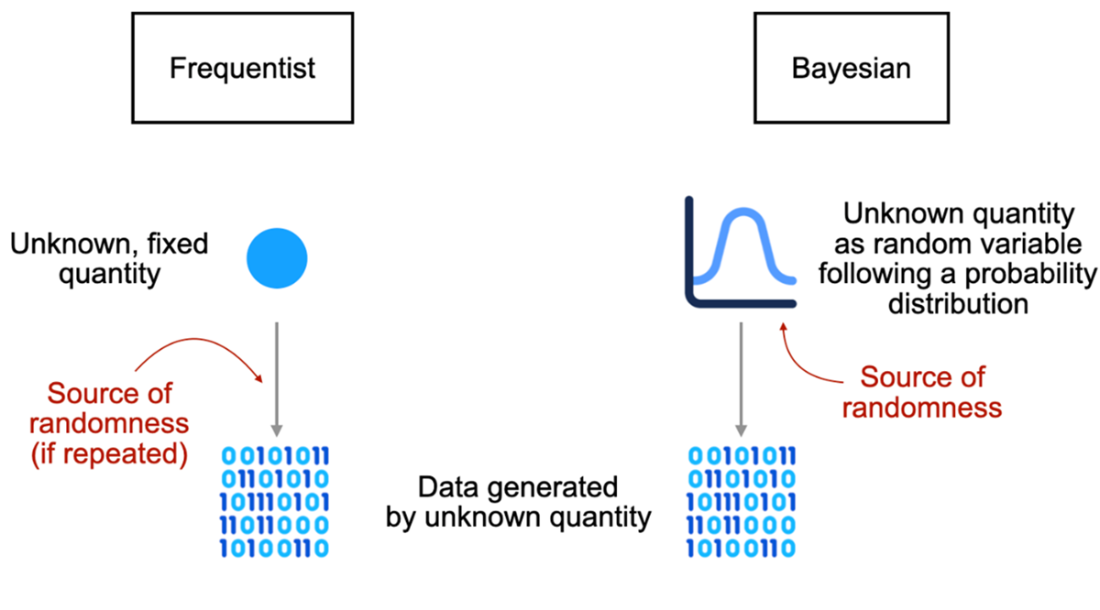
Bayesian probability interprets probability as degrees of belief about unknown quantities, encoded by probability distributions (e.g., a Bernoulli distribution with parameter p for “rain or not,” or a categorical distribution over rainfall amounts). Core probability rules (non-negativity, total probability equals one) and quantities like expected value enable concise summaries and credible statements about uncertainty. Crucially, Bayesian modeling formalizes belief updating: a prior belief is combined with data to produce a posterior distribution Pr(X | D). The chapter contrasts this with frequentist probability, which defines probability as long-run frequency and treats unknowns as fixed while randomness arises from data generation. Although both approaches can converge with abundant data, Bayesian methods explicitly incorporate prior knowledge, making assumptions transparent and enabling informed inference when data are scarce—at the cost of more modeling work and computation.

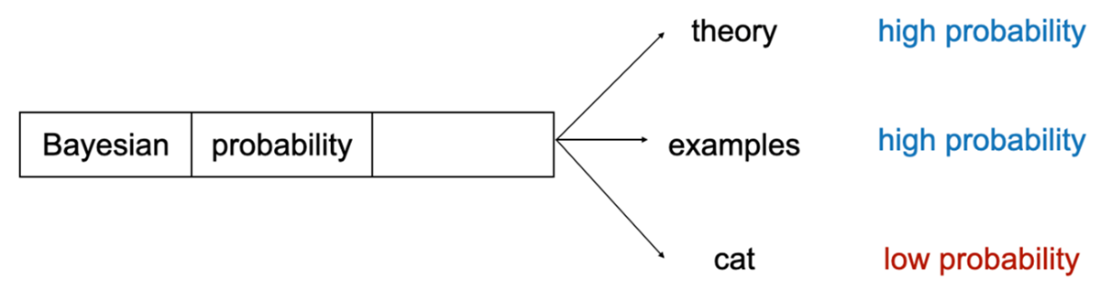
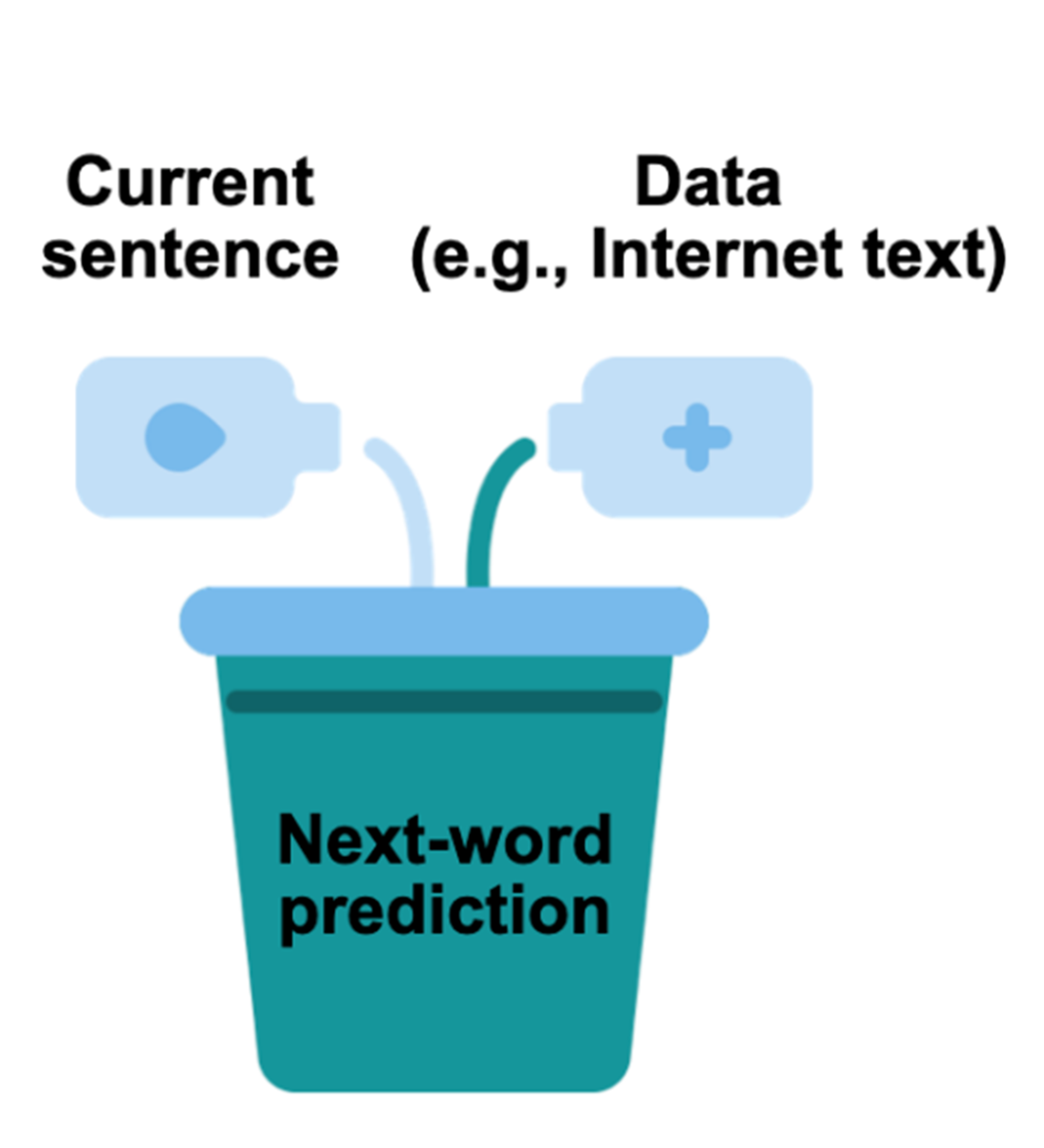
As a contemporary illustration, the chapter connects Bayesian thinking to large language models: next-word prediction is naturally a conditional probability task, and while LLMs are not fully Bayesian for computational reasons, they exploit probabilistic scoring, generate multiple plausible continuations, and leverage feedback to refine behavior. The chapter closes with guidance on method choice (Bayes for limited data, domain priors, and decision analysis; frequentist tools for abundant data and well-established procedures) and a roadmap for the book: foundations of priors, data, and posteriors; core techniques such as model comparison, hierarchical and mixture models, Monte Carlo and variational inference; specialized time-series and neural models; and Bayesian decision theory for principled choices under uncertainty.

An illustration of machine learning models without probabilistic reasoning capabilities being susceptible to noise and overconfidently making the wrong predictions.

An example categorical distribution for rainfall rate.

• We need probability to model phenomena in the real world whose outcomes we haven’t observed.
• With Bayesian probability, we use probability to represent our personal belief about an unknown quantity, which we model using a random variable.
• From a Bayesian belief about a quantity of interest, we can compute quantities that represent our knowledge and uncertainty about that quantity of interest.
• There are three main components to a Bayesian model: the prior distribution, the data, and the posterior distribution. The last component is the result of combining the first two and what we want out of a Bayesian model.
• Bayesian probability is useful when we want to incorporate prior knowledge into a model, when data is limited, and for decision-making under uncertainty.
• A different interpretation of probability, frequentism, views probability as the frequency of an event under infinite repeats, which limits the application of probability in various scenarios.
• Large language models, which power popular chat artificial intelligence models, apply Bayesian probability to predict the next word in a sentence.

FAQ