5 Fundamentals of machine learning

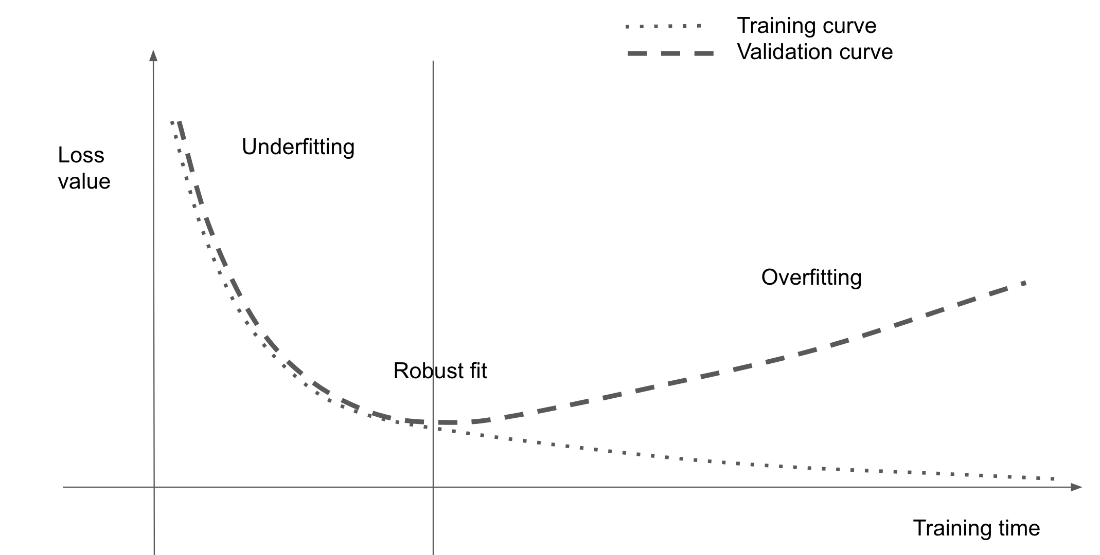
This chapter builds a practical and conceptual foundation for machine learning by centering on the tension between optimization and generalization. It explains how models learn to reduce training loss yet must be evaluated by how well they perform on unseen data, and it frames overfitting as the universal failure mode when optimization goes too far. The material emphasizes reliable evaluation and disciplined experimentation as the backbone of effective model development, setting expectations for how to read learning curves, recognize underfitting versus overfitting, and steer training toward robust, real-world performance.

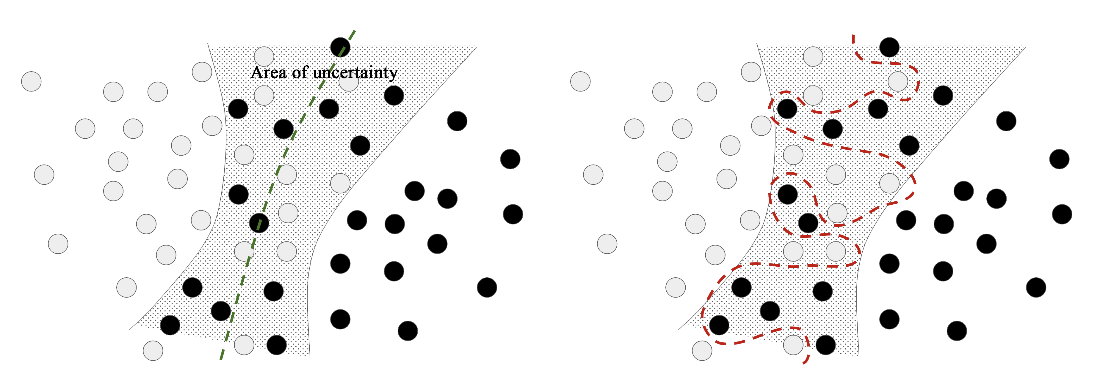
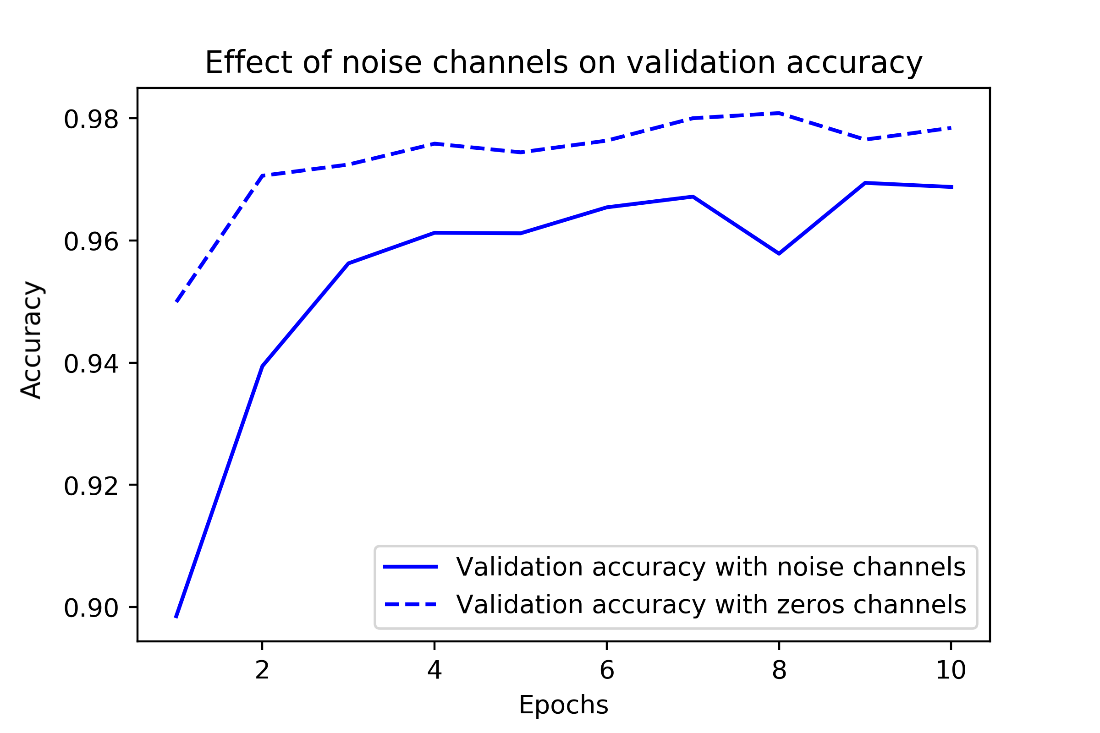
It then explores why overfitting happens and what enables generalization. Overfitting is amplified by noisy or mislabeled examples, inherently ambiguous targets, and rare features that invite spurious correlations. The chapter introduces the manifold hypothesis: natural data occupies low-dimensional, structured subspaces within high-dimensional input spaces, which lets deep networks generalize primarily by interpolating between training samples along these learned manifolds. Because deep models are smooth, highly expressive function approximators, they can memorize; but with good data and gradual training they also learn manifold structure well enough to interpolate. Consequently, data quality and coverage are paramount—dense, informative sampling of the input space is the most powerful lever for generalization; when data is limited, regularization is used to constrain memorization.

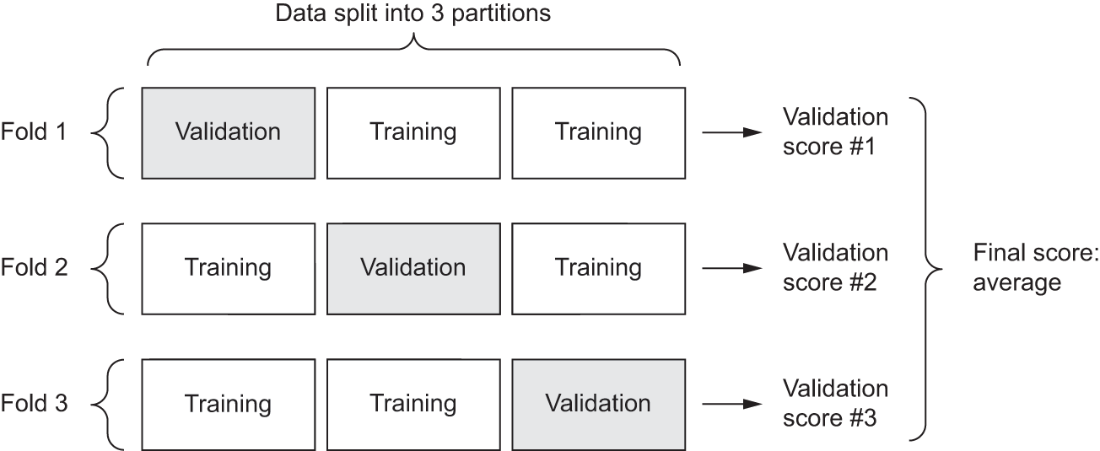
On measurement and practice, the chapter formalizes evaluation protocols: separate training, validation, and test splits; avoid information leaks; and use hold-out, K-fold, or iterated K-fold validation when data is scarce. It recommends establishing common‑sense baselines and guarding against pitfalls such as unrepresentative splits, temporal leakage, and duplicate samples across splits. To improve model fit, start by getting optimization to work (tune learning rate and batch size), select architectures with the right inductive biases for the modality, and increase capacity until overfitting is possible. To improve generalization, prioritize dataset curation and feature engineering, apply early stopping, and regularize via capacity control, weight penalties (L1/L2), and dropout. The overarching message: measure carefully, fit confidently, and regularize deliberately so that interpolation on well-structured data yields reliable performance.

Canonical overfitting behavior

Some pretty weird MNIST training samples

Mislabeled MNIST training samples

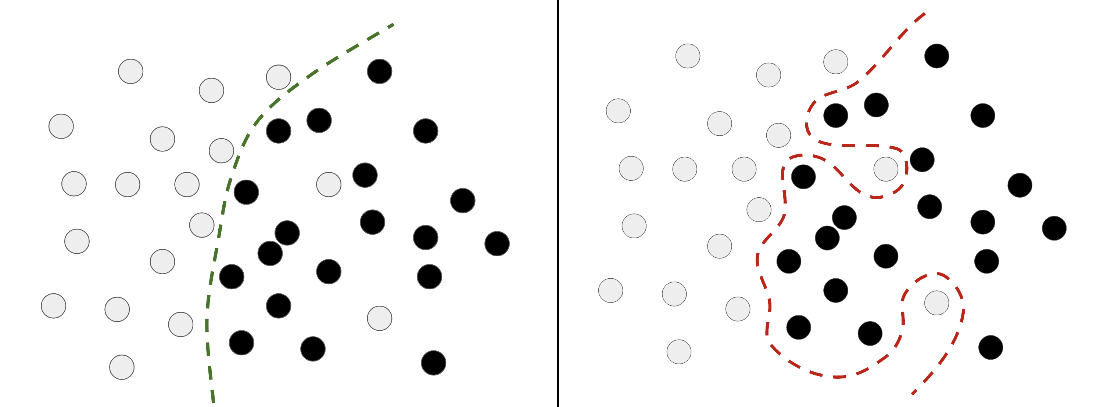
Dealing with outliers: robust fit vs. overfitting

Robust fit vs. overfitting giving an ambiguous area of the feature space

Effect of noise channels on validation accuracy

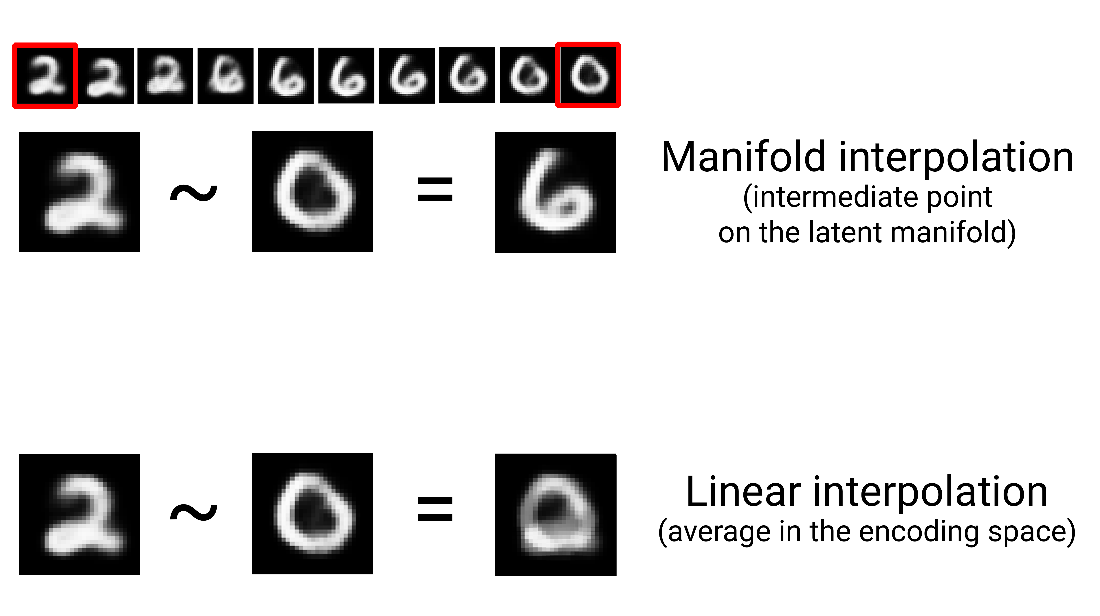
Different MNIST digits gradually morphing into one another, showing that the space of handwritten digits forms a “manifold”. This image was generated using code from Chapter 17.

Difference between linear interpolation and interpolation on the latent manifold. Every point on the latent manifold of digits is a valid digit, but the average of two digits usually isn’t.

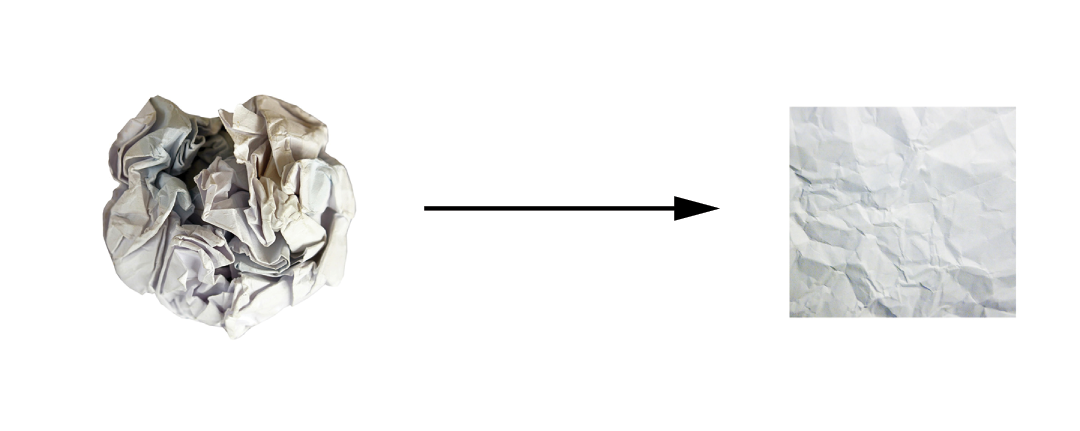
Uncrumpling a complicated manifold of data

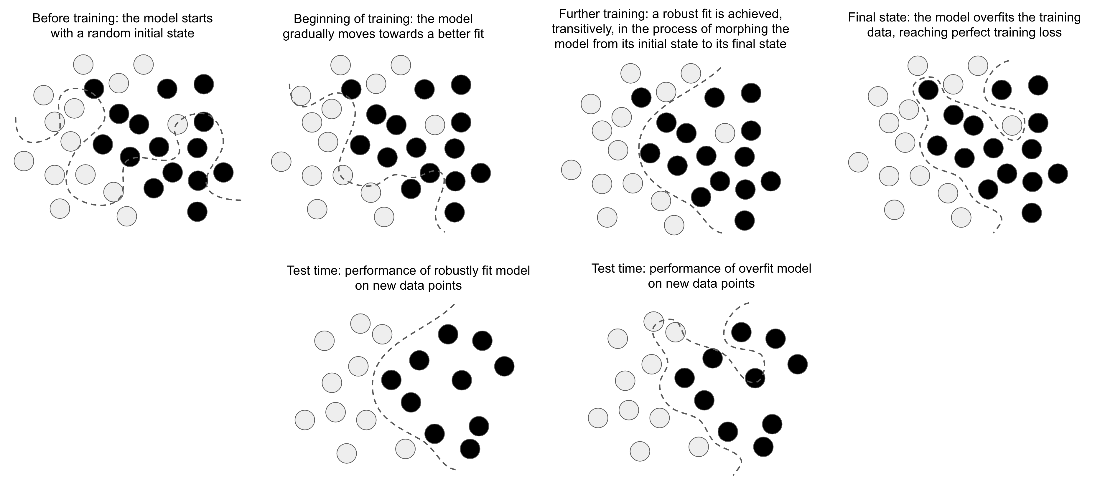
Going from a random model to an overfit model, and achieving a robust fit as an intermediate state

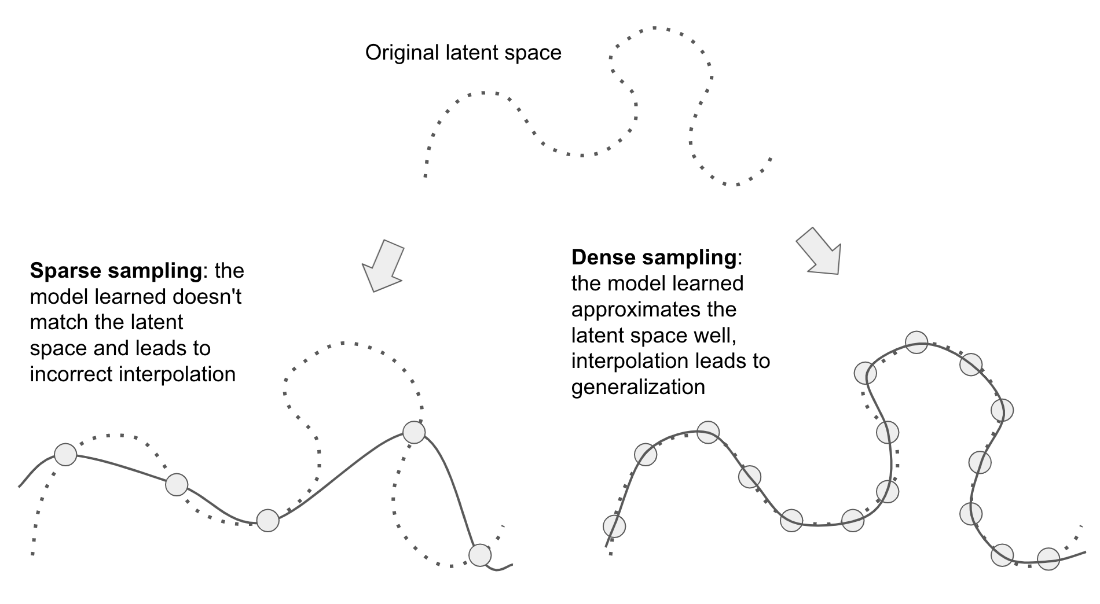
A dense sampling of the input space is necessary in order to learn a model capable of accurate generalization.

Simple hold-out validation split

Three-fold validation

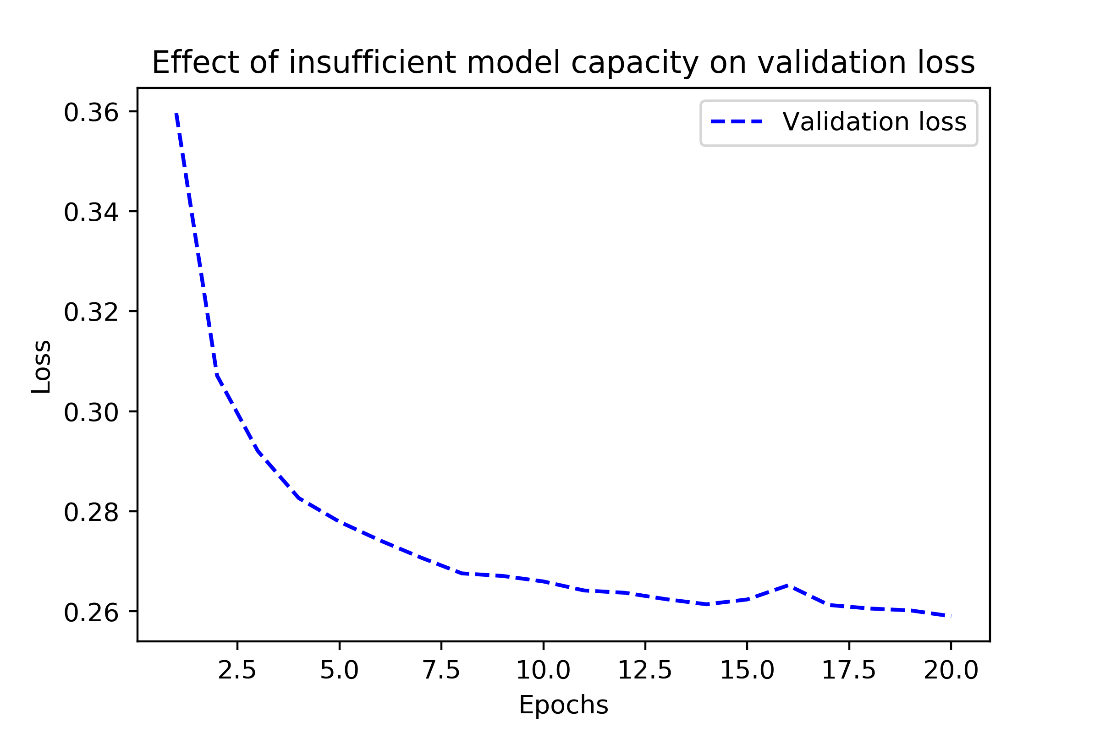
Effect of insufficient model capacity on loss curves

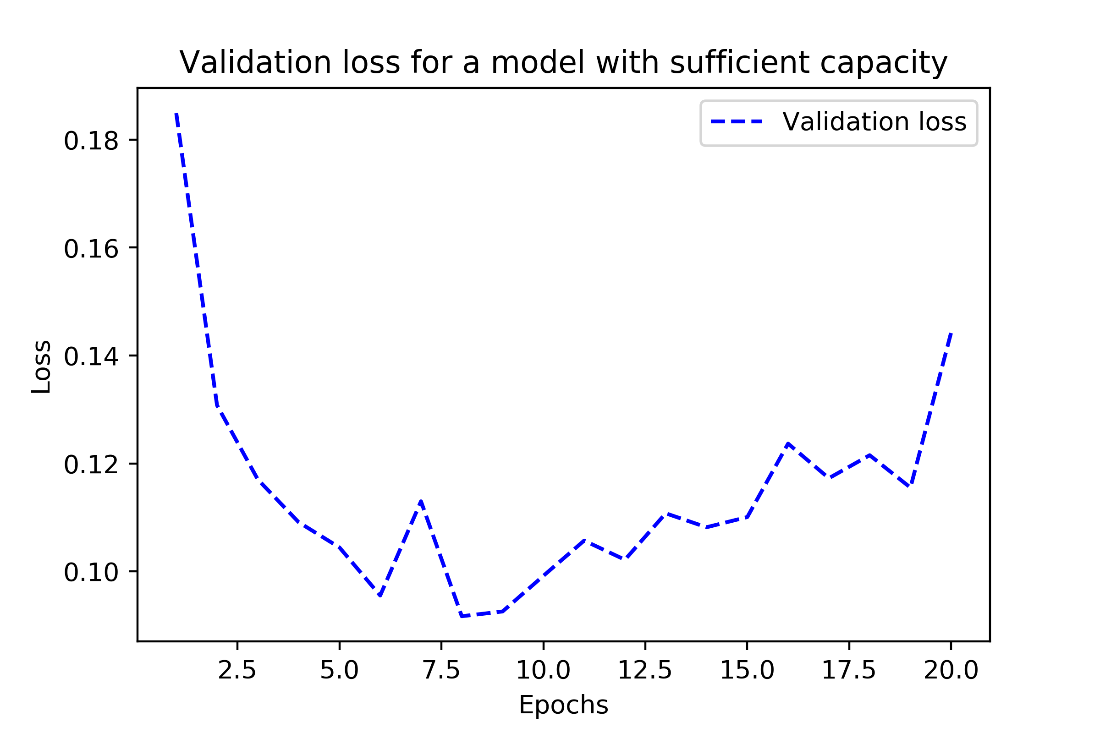
Validation loss for a model with appropriate capacity

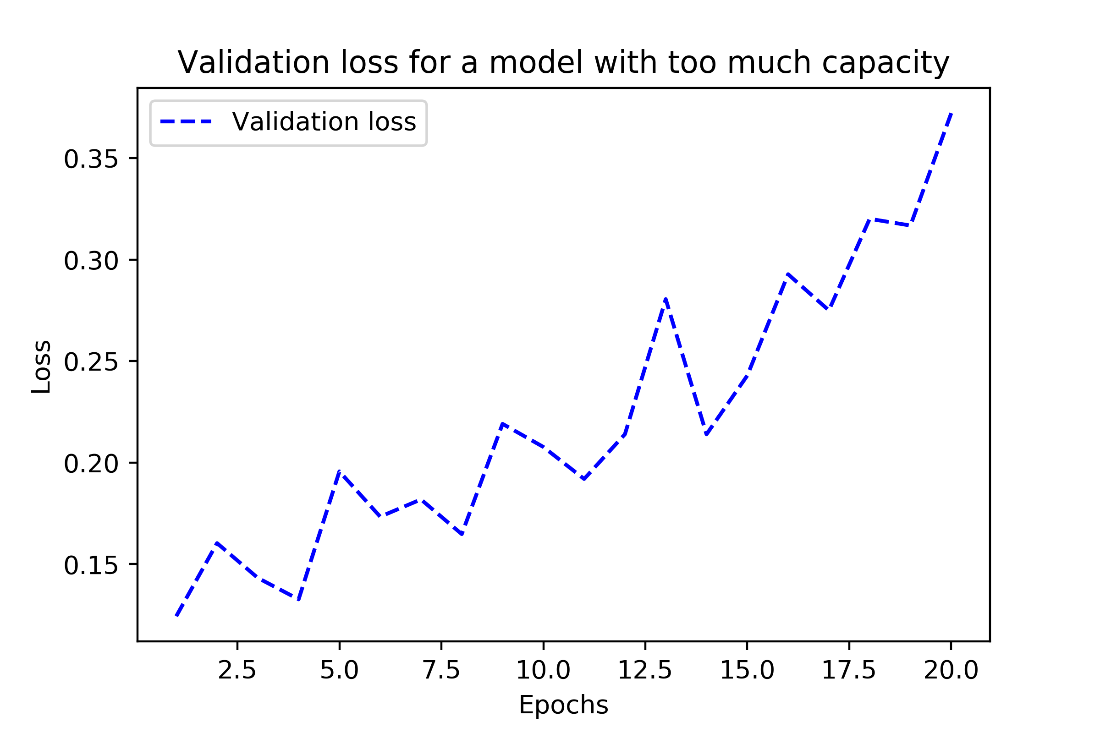
Effect of excessive model capacity on validation loss

Feature engineering for reading the time on a clock

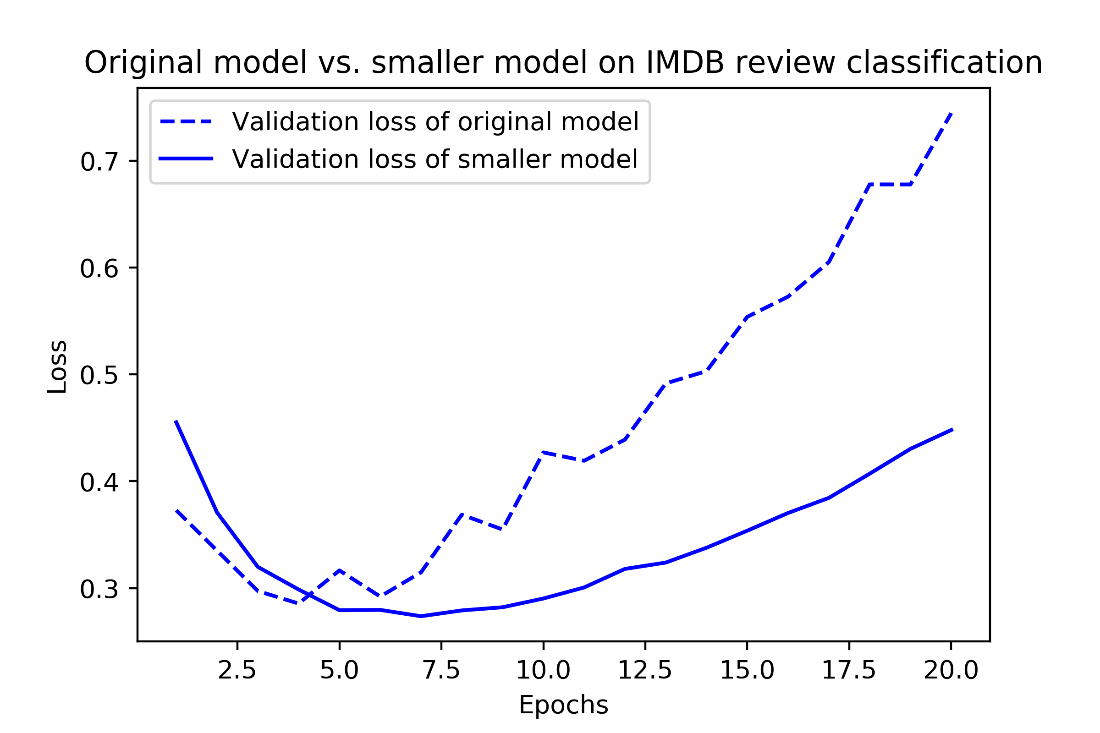
Original model vs. smaller model on IMDB review classification

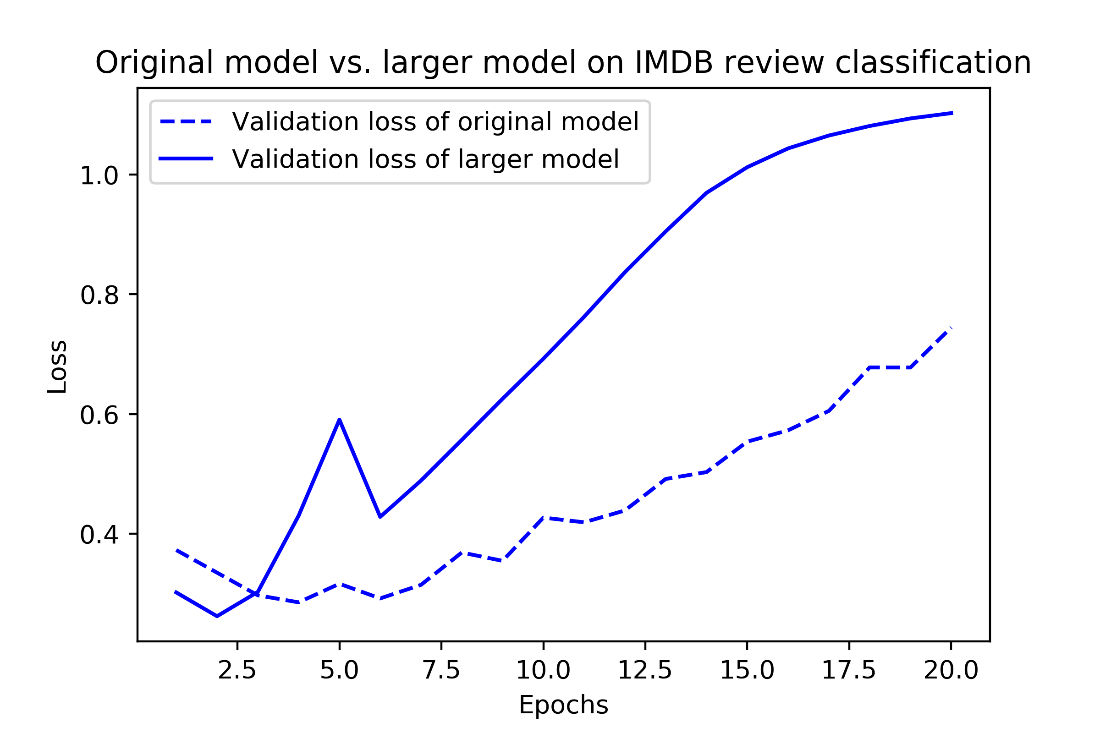
Original model vs. much larger model on IMDB review classification

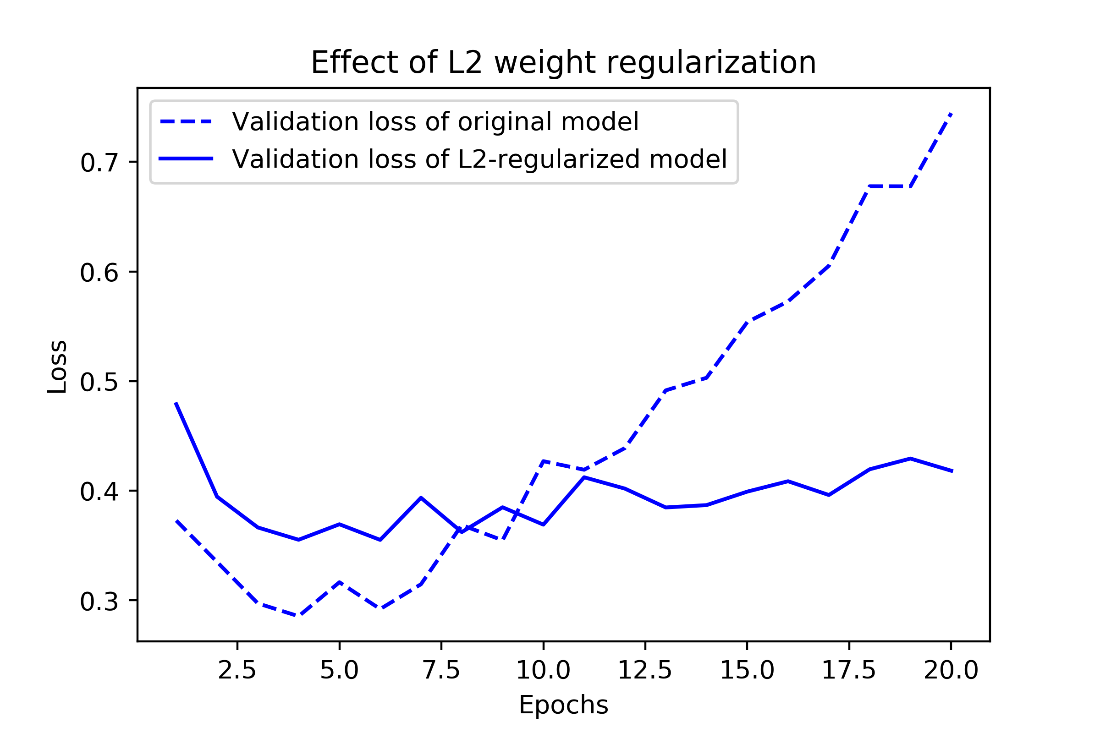
Effect of L2 weight regularization on validation loss

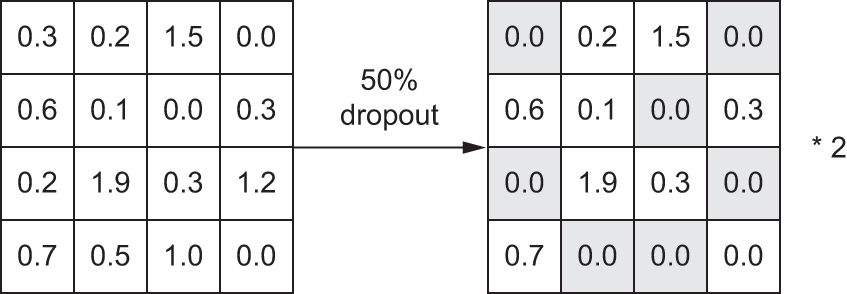
Dropout applied to an activation matrix at training time, with rescaling happening during training. At test time, the activation matrix is unchanged.

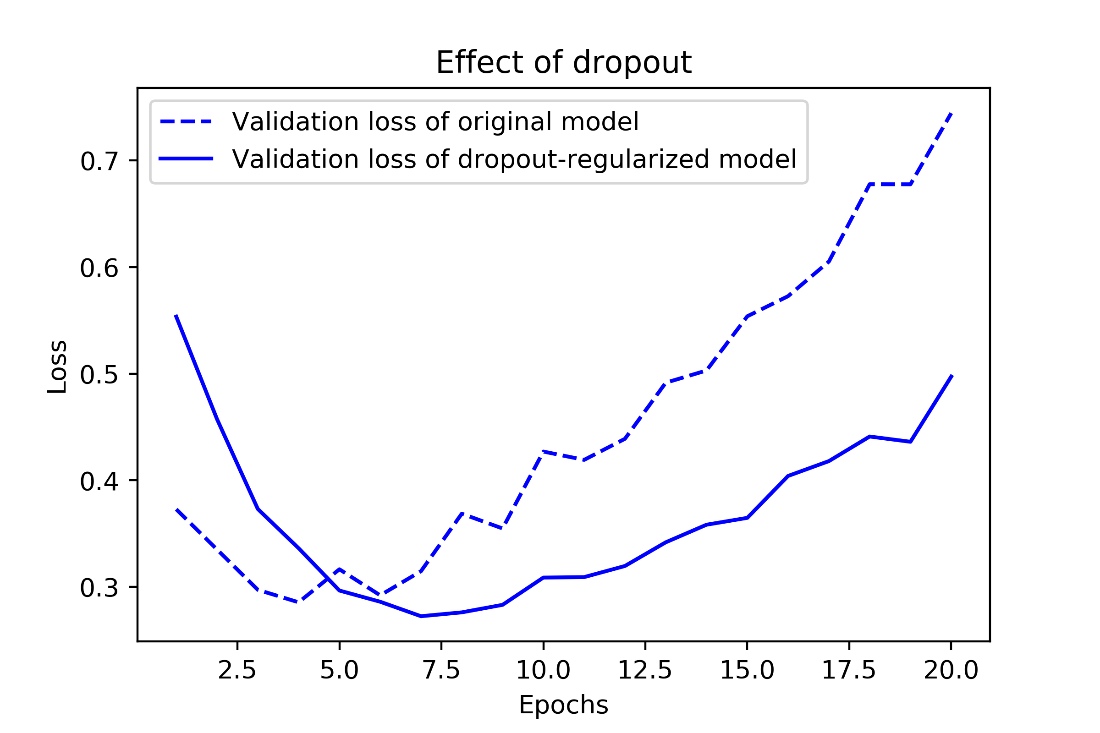
Effect of dropout on validation loss

• The purpose of a machine learning model is to generalize: to perform accurately on never-seen-before inputs. It’s harder than it seems.
• A deep neural network achieves generalization by learning a parametric model that can successfully interpolate between training samples – such a model can be said to have learned the latent manifold of the training data. This is why deep learning models can only make sense of inputs that are very close to what they’ve seen during training.
• The fundamental problem in machine learning is the tension between optimization and generalization: to attain generalization, you must first achieve a good fit to the training data, but improving your model’s fit to the training data will inevitably start hurting generalization after a while. Every single deep learning best practice deals with managing this tension.
• The ability of deep learning models to generalize comes from the fact that they manage to learn to approximate the latent manifold of their data, and can thus make sense of new inputs via interpolation.
• It’s essential to be able to accurately evaluate the generalization power of your model while you’re developing it. You have at your disposal an array of evaluation methods, from simple hold-out validation, to K-fold cross-validation and iterated K-fold cross-validation with shuffling. Remember to always keep a completely separate test set for final model evaluation, since information leaks from your validation data to your model may have occurred.
• When you start working on a model, your goal is first to achieve a model that has some generalization power and that can overfit. Best practices to do this include tuning your learning rate and batch size, leveraging better architecture priors, increasing model capacity, or simply training longer.
• As your model starts overfitting, your goal switches to improving generalization through model regularization. You can reduce your model’s capacity, add dropout or weight regularization, and use early stopping. And naturally, a larger or better dataset is always the number one way to help a model generalize.

FAQ