10 Encoding functions in quantum states
This chapter shows how to encode classical functions into quantum states so that measurements directly yield input–output pairs. Using two entangled registers—one for keys (inputs) and one for values (outputs)—the method builds a “quantum dictionary” in which each key is paired with its corresponding value. The approach extends phase/frequency encoding into a full function-encoding scheme and is illustrated on tasks such as summing the bits of an input, modeling the value and weight in a knapsack instance, and preparing function landscapes suitable for search.
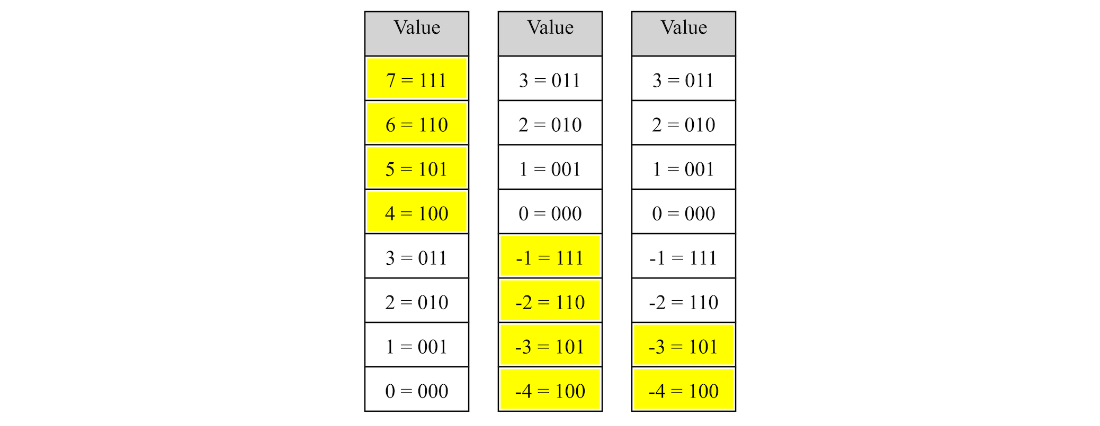
The core construction creates, for each key, a geometric-phase pattern across the value register via controlled phase rotations; an inverse quantum Fourier transform on the value qubits then maps these phases to the desired integer outputs. Linear and polynomial functions are handled uniformly by expressing them as polynomials of binary variables (monomials with coefficients and variable indices) and implementing each term with controlled or multi-controlled phase gates, plus an unconstrained phase for constants. The chapter discusses resource scaling in terms of input size, output size, and number of monomials, shows how to represent negative outputs with Two’s Complement, and demonstrates compact circuit templates and visual diagnostics that make the encodings transparent and reusable.
With a function encoded, Grover’s search amplifies target input–output pairs using simple, efficient oracles that match individual bits or multi-bit patterns in the value register (for example, selecting negatives, a numeric range, or the zero row). These oracles enable range queries, constraint filtering (as in knapsack), and root finding by tagging the all-zero output, with examples showing one-iteration amplifications and guidance on iteration counts via quantum counting or adaptive schedules. Altogether, the chapter provides a practical recipe: encode a function once, then query it quantumly to locate values of interest—thresholds, ranges, negatives, or zeros—using lightweight Grover oracles.
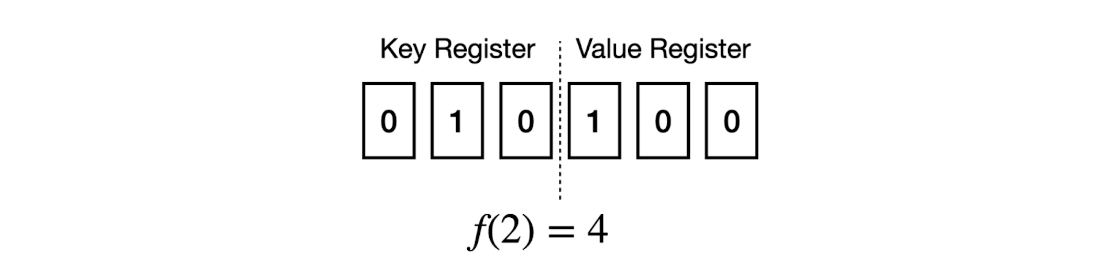
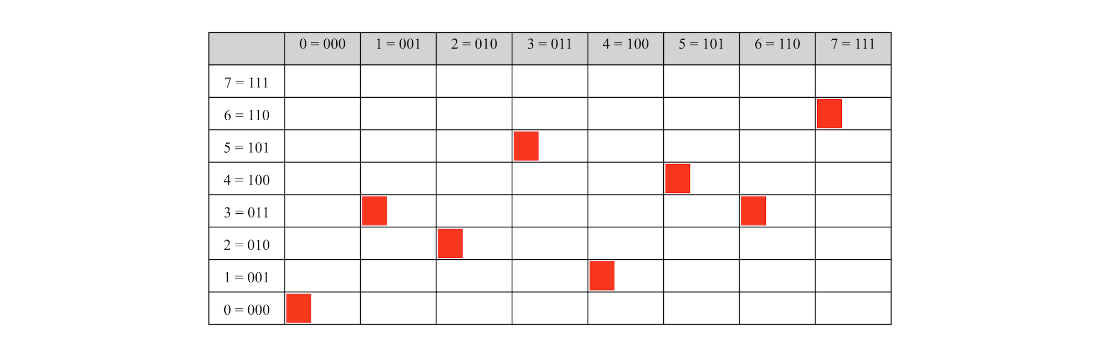
An example measurement outcome of a quantum state with \(n = 3\) key qubits and \(m = 3\) value qubits and an encoded function \(f\) representing the input-output pair \((2, 4)\).
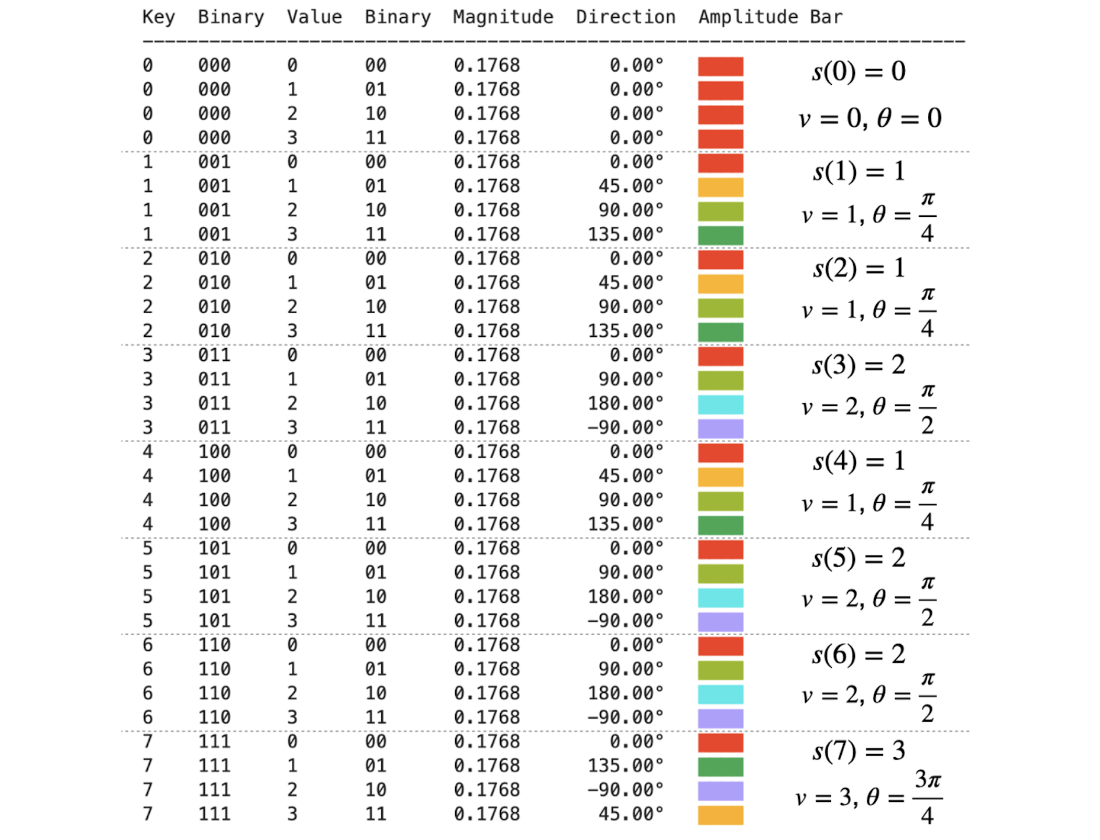
A quantum state where the value register encodes a geometric sequence for each key. The angle parameter of a geometric sequence reflects the value corresponsing to its key.
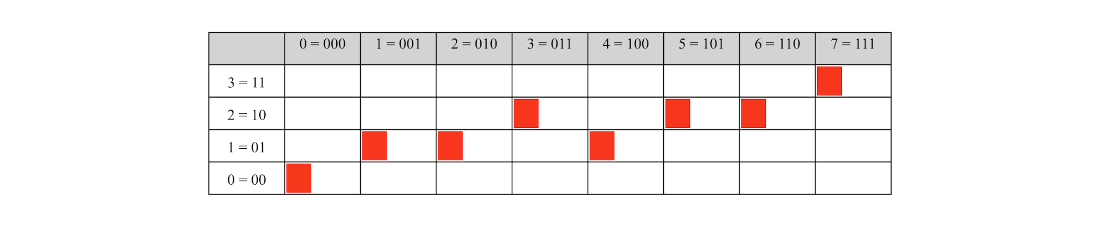
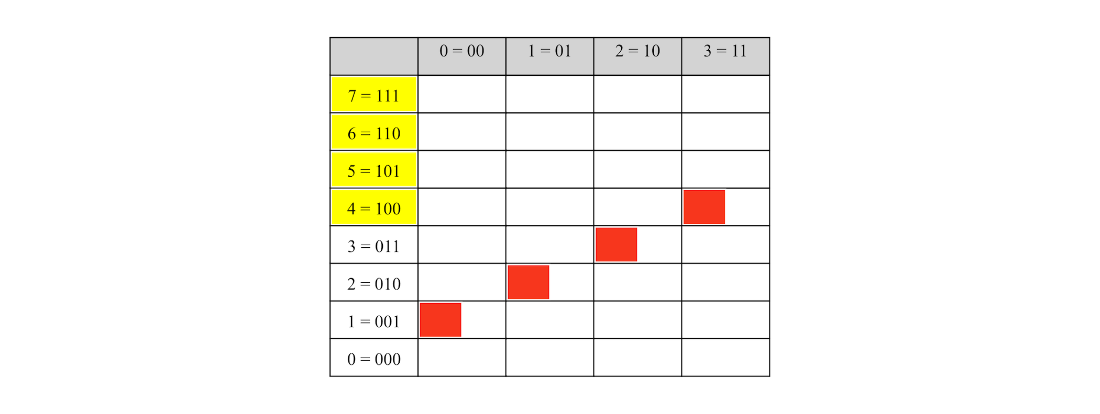
Grid visualization of the encoded function inputs (columns) and outputs (rows).
Three registers encoding an item selection, its total value, and its total weight for solving the knapsack problem.

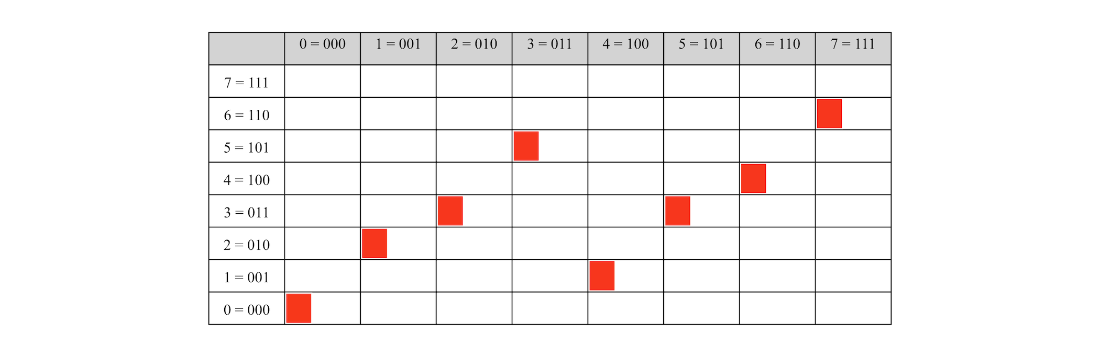
The value (rows) of each possible knapsack selection (columns).
The weight (rows) of each possible knapsack selection (columns).
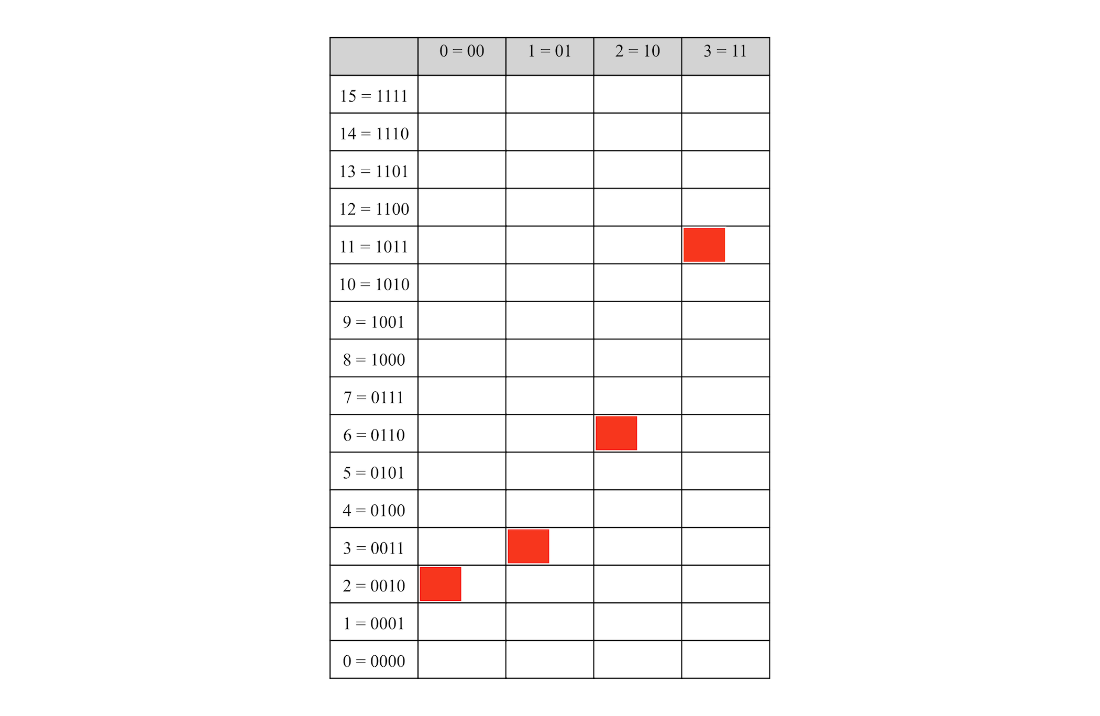
TThe quantum state encoding the function \(f(k) = k^2 + 2\) where \(0 \le k < 3\).
The quantum state encoding the function \(f(k) = k^2 - 5k + 7\) where \(0 \le k < 3\).
The quantum state encoding the function \(f(k) = k^2 -3\), for \(0 \le k < 3\).
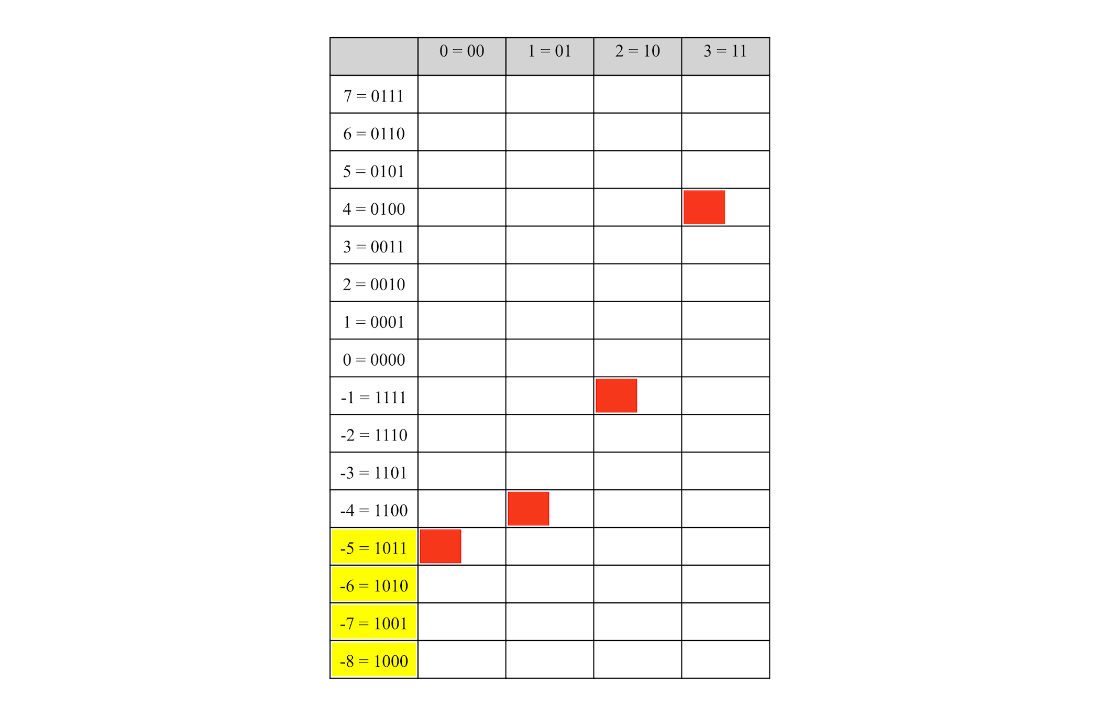
(Left) Values identified by an oracle that matches 1 in the first digit. (Center) Values (using Two’s Complement) identified by an oracle that matches 1 in the first digit. (Right) Values (using Two’s Complement) identified by an oracle that matches 1 in the first digit and 0 in the second digit.
The quantum state encoding the function \(f(k) = k + 1\), for \(0 \le k < 3\). The values that meet our search criteria are highlighted.
The result of applying a Grover iteration to the quantum state encoding the function \(f(k) = k + 1\), for \(0 \le k < 3\), with an oracle that tags outcomes with 1 as the first digit in the value register.
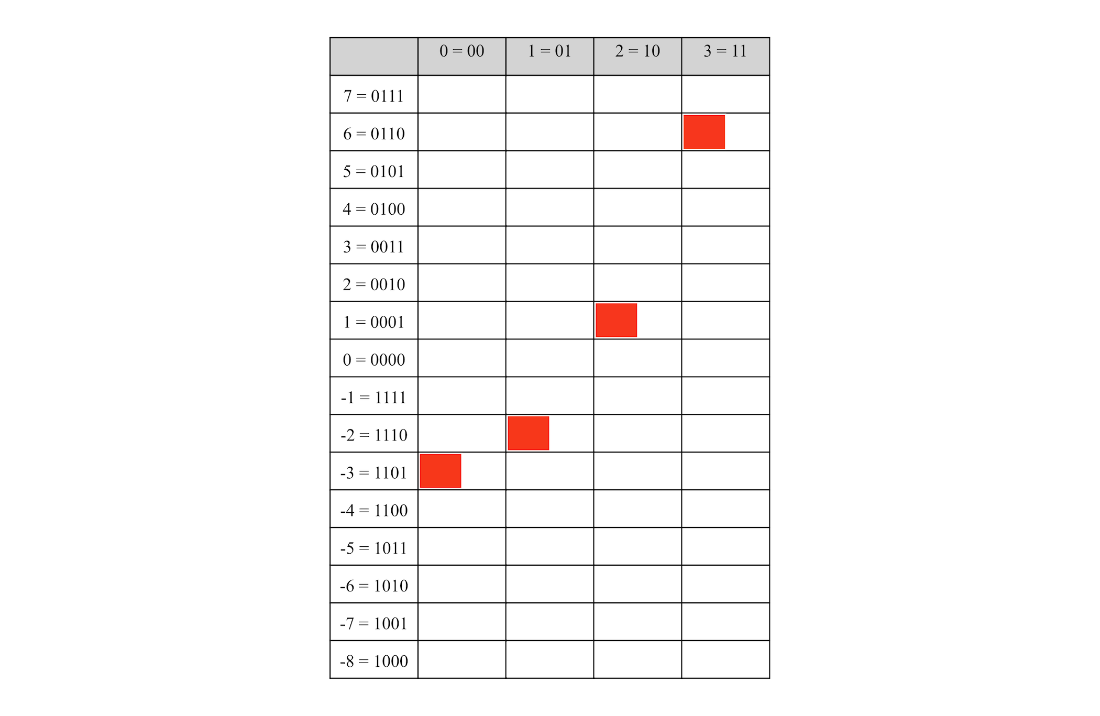
The quantum state encoding the function \(f(k) = k^2 - 5\), for \(0 \le k < 3\). The values that meet the search criteria are highlighted.
The result of applying a Grover iteration to the quantum state encoding the function \(f(k) = k^2 - 5\), for \(0 \le k < 3\), with an oracle that tags outcomes with 1 as the first digit and 0 as the second digit in the value register.
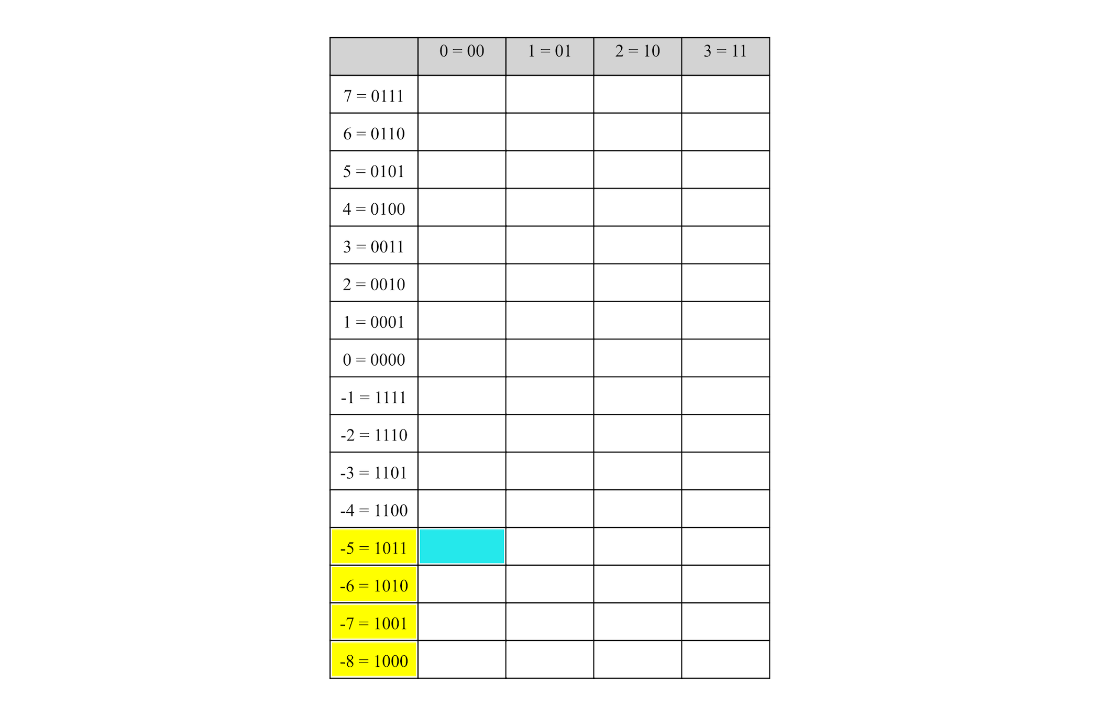
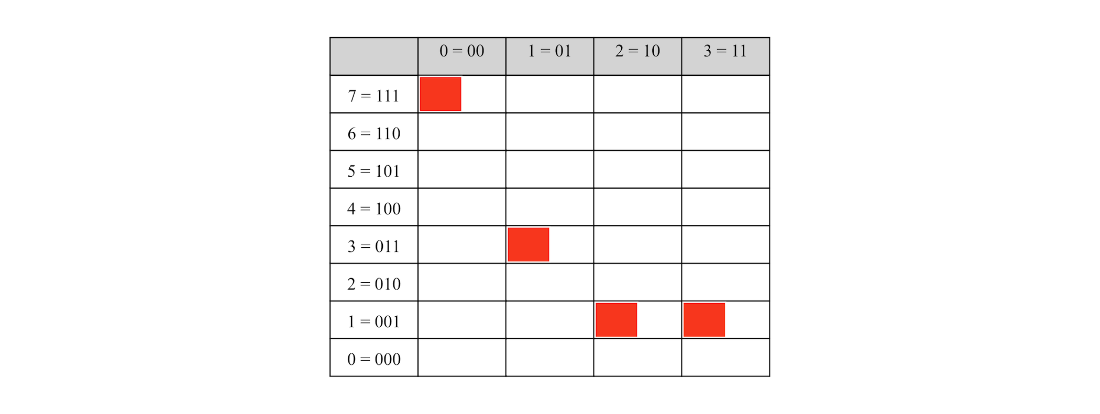
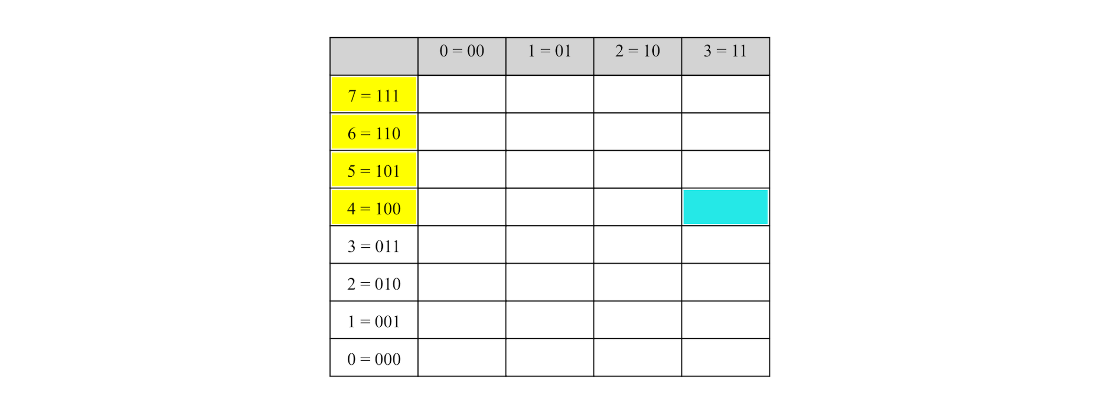
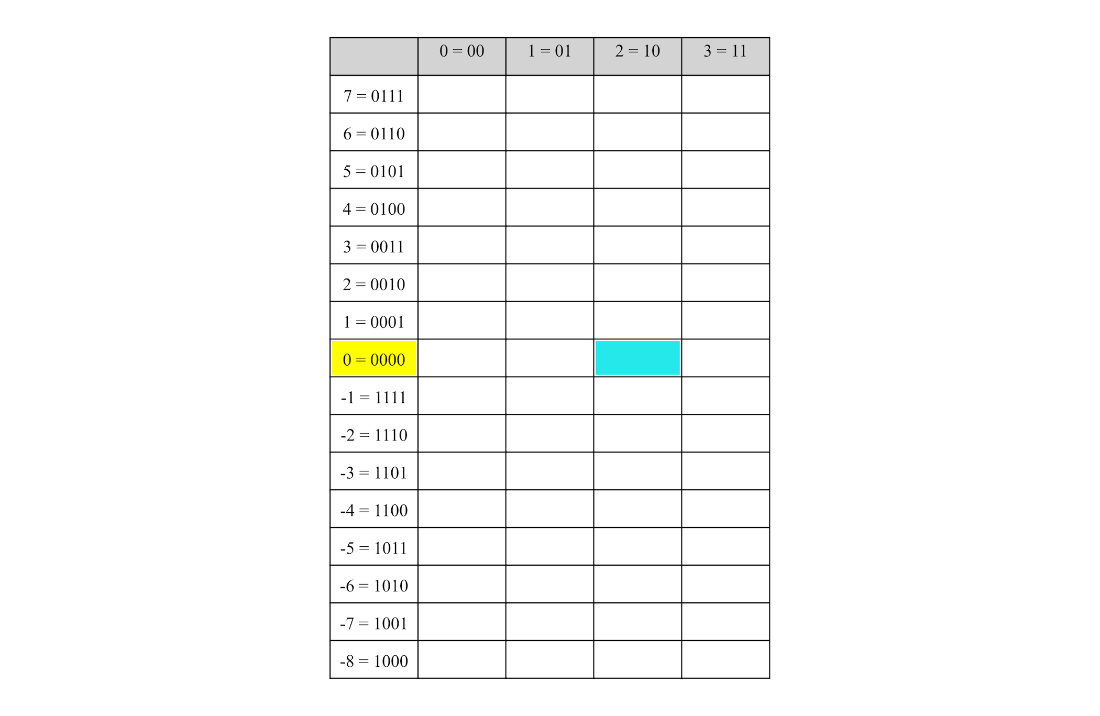
The quantum state encoding the function \(f(k) = k^2 - 4\) where \(0 \le k < 3\). The value register corresponding to outcome 0 is highlighted.
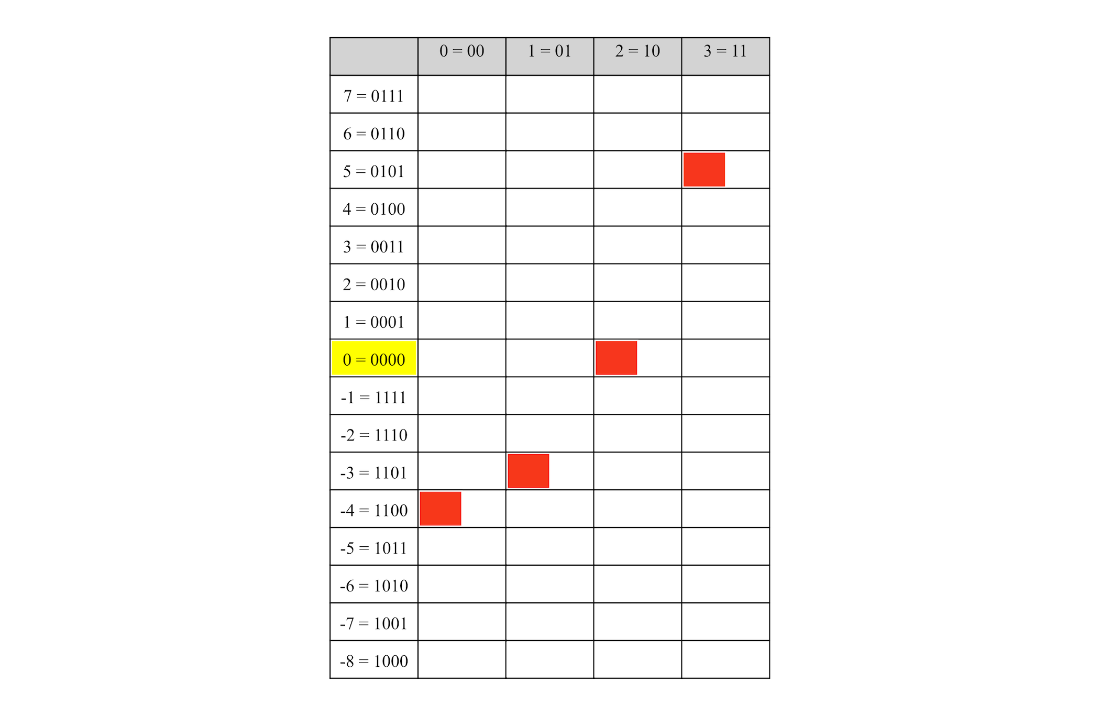
The result of applying a Grover iteration to the quantum state encoding the function \(f(k) = k^2 - 4\), for \(0 \le k < 3\), with an oracle the zero outcome in the value register.
Summary
- We can encode key-value pairs in a quantum state using two registers of qubits. The key and value registers can represent the inputs and outputs of a function. We entangle the registers so that if a measurement is performed, the outcome will contain a key paired with its corresponding value.
- We encode values in the value register by preparing a periodic quantum state with an angle determined by the encoded value, followed by the IQFT.
- We can use a Grover operator to find desired output values, such as inputs where the function is zero.
FAQ
What is a “quantum dictionary” and how are key–value pairs represented in a quantum state?
Two entangled qubit registers encode integer input–output pairs: the key register holds inputs and the value register holds corresponding outputs. Preparing a superposition over keys and entangling it with values ensures that a measurement yields a key alongside its matching value.How does the frequency/value encoding with the inverse QFT (IQFT) work?
- Put the value register in equal superposition.- Impose a geometric phase progression whose step is proportional to the integer value you want to encode (via controlled phase rotations).
- Apply the IQFT on the value register to convert those phases into the binary representation of the integer output.
How many qubits do I need for the key and value registers?
If the key register has n qubits, you can address 2^n integer inputs. If the value register has m qubits, you can represent outputs in a range of 2^m integers (with optional Two’s Complement for negatives). Choose n from the input domain size and m from the output range size.How do I encode a simple function like the “sum of bits” in the key?
Create superpositions on both registers, then for each key qubit that is 1, apply controlled phase rotations onto each value qubit so the value register’s phases advance by a step proportional to the sum of the key’s 1-bits. Finish with the IQFT on the value register to read out the sum as an integer.How are linear functions (e.g., knapsack weights/values) encoded?
Express the linear function as terms of the form (coefficient, [variable indices]). For each term:- Apply controlled phase gates from the listed key qubit(s) onto each value qubit with angles proportional to the coefficient.
- Apply the IQFT on the value register.
This maps each key (e.g., item selection) to its linear outcome (e.g., total value or weight).
How do I encode polynomial functions of binary variables?
Rewrite the function as a polynomial over binary variables k_j ∈ {0,1}. Represent each monomial as (coeff, [indices]). Then:- Use multi-controlled phase gates (mcp) when a term has multiple variables, single-controlled (cp) for one variable, and an uncontrolled phase for constants.
- Apply the IQFT on the value register. This generalizes encoding from linear to polynomial functions.
How are negative outputs represented?
Use Two’s Complement on the value register. With m value qubits, strings starting with 0 represent [0, 2^(m−1)−1], and those starting with 1 represent [−2^(m−1), −1]. The encoding steps are the same; only the interpretation of the value bits changes.How can Grover’s algorithm help search for specific function values or ranges?
After preparing the encoded state, build an oracle that tags outcomes matching desired value bits (e.g., first value bit = 1 for upper-half values, or for negatives under Two’s Complement). Combine the prepare circuit, the oracle, and Grover’s diffusion to amplify target key–value pairs, then measure.What is the gate complexity of a polynomial-encoding circuit?
With an n-qubit key register, an m-qubit value register, and t monomials:- Superposition/encoding uses n + m Hadamards and m·t controlled phase gates.
- The IQFT adds m Hadamards and m(m−1)/2 controlled phase gates.
Total gates: n + (t + 2)·m + m(m−1)/2 (counting only these gate types).
 Building Quantum Software with Python ebook for free
Building Quantum Software with Python ebook for free