1 Web dev math fundamentals
Math quietly powers most of what front-end designers and developers do, from sizing text and spacing components to animating motion and positioning elements in the viewport. While you can ship interfaces without thinking about equations, understanding the small amount of practical math behind CSS and JavaScript dramatically improves precision, resilience, and performance. This chapter lays a hands-on foundation, showing how a little math sharpens layouts, smooths animations, and makes responsive behavior predictable—no advanced theory required.
It explains why math matters: it turns guesswork into reliable spacing and alignment, accelerates responsive design by clarifying how percentages, viewport units, and functions like clamp behave, and enables lighter, smarter code and faster debugging. The chapter distinguishes CSS’s declarative, built-in math (units, calc, min/max/clamp, easing curves) from JavaScript’s dynamic, procedural capabilities (the Math object, real-time calculations, interaction-driven logic), and shows when each tool is the right fit—often in combination—to achieve adaptable, maintainable interfaces.
Finally, it surveys the essential concepts you’ll use daily: basic arithmetic and expressions; algebra with variables drawn from the environment; ratios for aspect ratios, grid fractions, and typographic scales; exponents and roots for easing and distance; linear equations for steady motion and scroll progress; inequalities for conditions and breakpoints; geometry for points, vectors, angles, shapes, and transforms; trigonometry for circular layouts, rotations, and wave-like motions; and coordinate systems anchored to the viewport. By learning to spot these patterns, you gain control over behavior and polish—building interfaces that are more consistent, responsive, accessible, and delightful.
Why is the section heading so much bigger than the main heading? Math!

A type scale based on the Golden Ratio (approximately 1.618).

Centering an element within its containing block requires just a few CSS declarations, but behind the scenes the browser is jumping through many mathematical hoops to get the job done
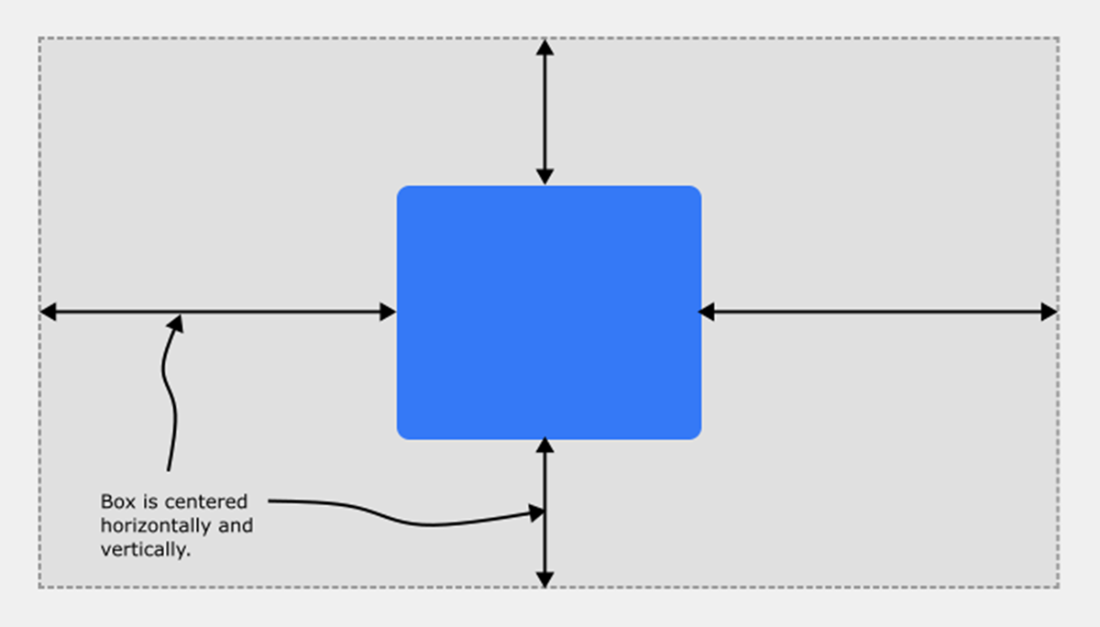
Some basic geometric figures.
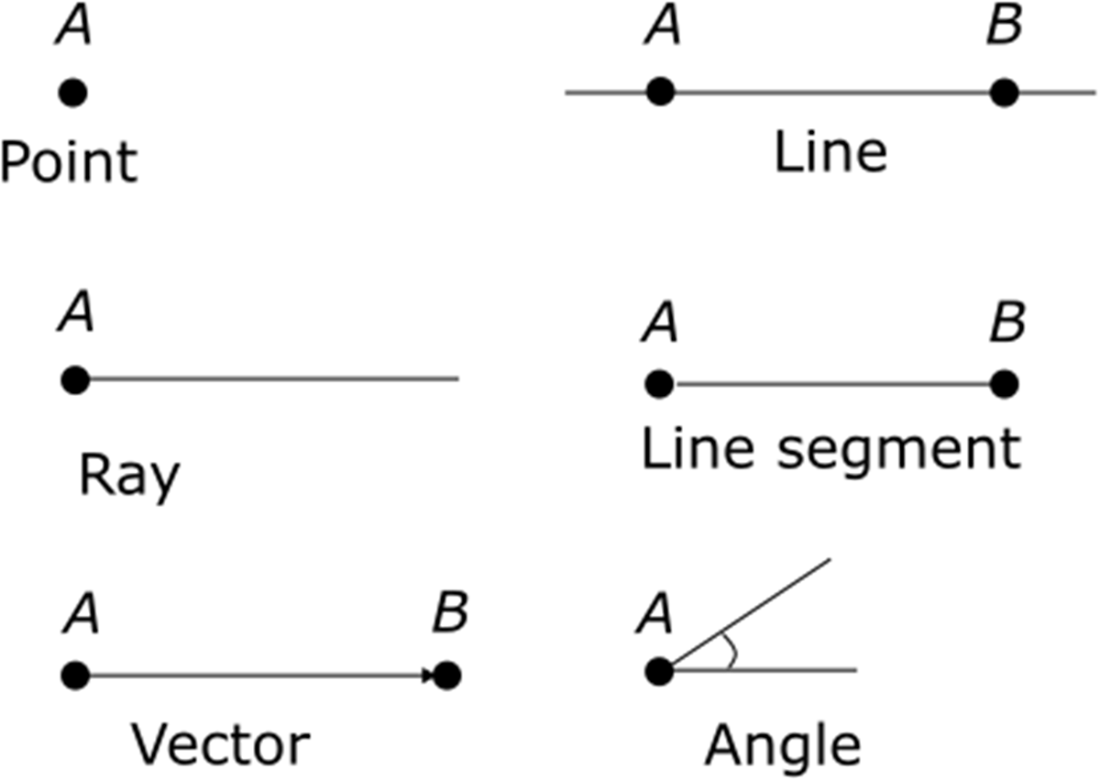
A right triangle and its sides relative to the angle theta (θ).
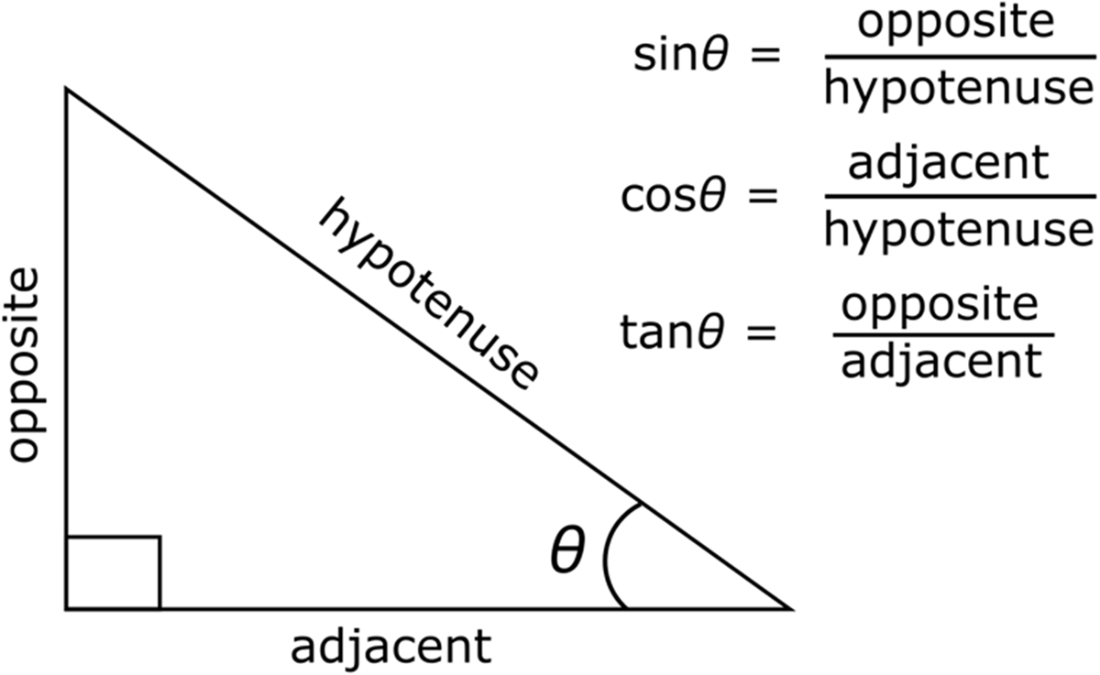
Using trigonometry to arrange menu items in a circle.
Summary
- Learning about front-end math will help you build more precise and reliable layouts, write more performant code, and debug layout issues faster.
- Mathematics in UI and UX design has practical use cases for responsive layouts, typography, colors, and spacing and alignment.
- Developers use math when coding motion and animation, layouts, and user interactions.
- In CSS, you use math to position and transform elements, scale layouts, build responsive elements, style text, and animate transitions.
- CSS provides math functions that you can use to perform basic arithmetic right in your style declarations.
- JavaScript gives you full control with dynamic, real-time math using the Math object and custom logic.
- Use CSS math for layout, sizing, spacing, and typography when the values can be determined by the browser at render time.
- Use JavaScript math when you need interaction, animation, or real-time adjustments based on user behavior or complex conditions.
FAQ
Why should a front-end designer or developer learn “web dev math”?
It makes layouts more precise and reliable, speeds up responsive design, improves performance (less reliance on heavy libraries), simplifies debugging, unlocks creative patterns (grids, type scales, circular layouts), and increases professional value by bridging design intuition with technical rigor.
Where does math show up in everyday UI/UX work?
- Responsive layouts: percentages, viewport units, and calc()
- Typography: modular scales and ratios (for rhythm)
- Color: numeric manipulation for contrast, blending, and brightness
- Spacing and alignment: grids, gutters, fractions
- Motion: easing curves, timing functions, velocity equations
Why can two h2 elements with font-size: 2em render at different sizes?
The em unit is relative to the computed font size of the element’s parent. In nested contexts, em values compound. For example, if a parent sets font-size to 1.75em and the h2 uses 2em, the result is 1.75 × 2 = 3.5em relative to the ancestor’s base, which can be much larger than a sibling h2 whose parent font-size is smaller. Use rem for root-relative sizing when you need consistency.
When should I use CSS math vs JavaScript math?
- Use CSS (calc, min, max, clamp) for declarative, render-time layout, spacing, and typography that the browser can compute from context.
- Use JavaScript (Math, custom logic) for interactive, stateful, or real-time behaviors: advanced animations, physics, user input, and conditional logic.
- Often you’ll combine both: CSS for design/scale; JS for behavior/dynamics.
Which CSS functions are essential for responsive, math-driven design?
- calc(): combine units and do basic arithmetic
- min() / max(): cap values at upper/lower bounds
- clamp(min, preferred, max): fluid values with safe limits
- aspect-ratio: maintain width:height relationships
What’s the “minimum math” I need to build better interfaces?
- Arithmetic and expressions (+ − × ÷)
- Algebra (variables, functions, solving for unknowns)
- Ratios (aspect ratios, fr units, modular type scales)
- Exponents and roots (easing, distances, growth/decay)
- Linear equations (y = mx + b for scroll, speed, scaling)
- Inequalities and comparisons (breakpoints, bounds, conditions)
- Geometry (points, lines, angles, transforms, shapes)
- Trigonometry (sin, cos, tan for circular/oscillatory motion)
- Coordinate systems (viewport origin, clientX/Y, bounding rects)
How do ratios help with typography and layout?
- Typography: build modular scales with a ratio (e.g., 1.2 or 1.618) to keep rhythm and hierarchy.
- Aspect ratio: preserve media proportions (e.g., 16/9 with aspect-ratio).
- Grids: distribute space with fractional units (e.g., 3fr 2fr 1fr).
How are linear equations used in interfaces?
They map one changing value to another at a constant rate (y = mx + b). Examples:
- Scroll progress: progress = scrollY / totalHeight
- Constant motion: position = initial + speed × time
- Fluid sizes: width = 0.5 × viewport + offset (e.g., calc(50vw + 20px))
How do trigonometric functions show up in UI work?
- Positioning items around a circle: x = cx + r cos(θ), y = cy + r sin(θ)
- Oscillations and waves: translateY( A × sin(t × f) )
- Circular paths and rotations: angles, arcs, and periodic motion
What is the viewport coordinate system and why does it matter?
It’s a 2D system with origin (0,0) at the top-left of the viewport; x increases rightward, y downward, usually in pixels. It underpins absolute/fixed positioning, pointer events (clientX/Y), element measurements (getBoundingClientRect), and viewport units (vw/vh) for full-bleed sections and fluid typography.
 Math for Web Design ebook for free
Math for Web Design ebook for free